题目内容
【题目】已知:如图,∠1=∠2,∠C=∠D。
求证:∠A=∠F。
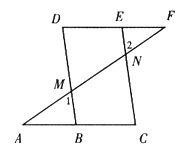
证明:∵∠1=∠2(已知),
又∠1=∠DMN(_______________),
∴∠2=∠_________(等量代换),
∴DB∥EC( ),
∴∠DBC+∠C=1800(两直线平行 , ),
∵∠C=∠D( ),
∴∠DBC+ =1800(等量代换),
∴DF∥AC( ,两直线平行),
∴∠A=∠F( )
【答案】对顶角相等;DMN;同位角相等,两直线平行;同旁内角互补;已知;∠D;同旁内角互补;
两直线平行 ,内错角相等.
【解析】试题分析:由∠1=∠2,∠1=∠DMN,根据同位角相等,两直线平行,易证得DB∥EC,又由∠C=∠D,易证得AC∥DF,继而证得结论.
试题解析:证明:∵∠1=∠2(已知),
又∠1=∠DMN(_对顶角相等),
∴∠2=∠_DMN_(等量代换),
∴DB∥EC( 同位角相等,两直线平行 ),
∴∠DBC+∠C=1800(两直线平行 , 同旁内角互补 ),
∵∠C=∠D( 已知 ),
∴∠DBC+ ∠D =1800(等量代换),
∴DF∥AC( 同旁内角互补 ,两直线平行),
∴∠A=∠F( 两直线平行 ,内错角相等 )
故答案为:对顶角相等;DMN,同位角相等,两直线平行;∠ABD=∠C;两直线平行,同位角相等;∠ABD=∠D;等量代换;内错角相等,两直线平行;(两直线平行,内错角相等).

练习册系列答案
相关题目