题目内容
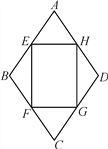
【题目】如图，四边形ABCD是一个菱形绿地，其周长为40
m，∠ABC＝120°，在其内部有一个四边形花坛EFGH，其四个顶点恰好在菱形ABCD各边的中点，现在准备在花坛中种植茉莉花，其单价为10元/m2，请问需投资金多少元？(结果保留整数)
【答案】866元
【解析】分析：连接BD，AC，由菱形ABCD的周长求出边长，再由∠ABC的度数确定出三角形ABD与三角形BCD都为等边三角形，进而求出BD与AC的长，由E、F、G、H分别为中点确定出四边形EFGH为矩形，求出矩形边长，进而求出矩形面积，求出所求即可．
详解：连接BD，AC．
∵菱形ABCD的周长为40
m，∴菱形ABCD的边长为10m．
∵∠ABC=120°，∴△ABD，△BCD是等边三角形，∴对角线BD=10m，AC=10
m．
∵E，F，G，H是菱形ABCD各边的中点，∴四边形EFGH是矩形，矩形的边长分别为5m，5m，∴矩形EFGH的面积为5×5=50
（m2），即需投资金为50×10=500≈866（元）．
答：需投资金为866元．
练习册系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
【题目】水果店以每箱60元新进一批苹果共400箱，为计算总重量，从中任选30箱苹果称重，发现每箱苹果重量都在10千克左右，现以10千克为标准，超过10千克的数记为正数，不足10千克的数记为负数，将称重记录如下：
规格 | ﹣0.2 | ﹣0.1 | 0 | 0.1 | 0.2 | 0.5 |
筐数 | 5 | 8 | 2 | 6 | 8 | 1 |
（1）求30箱苹果的总重量
（2）若每千克苹果的售价为10元，则卖完这批苹果共获利多少元
