Question

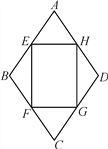
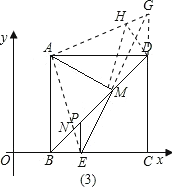
【题目】如图，四边形ABCD位于平面直角坐标系的第一象限，B、C在x轴上A点函数上，且AB∥CD∥y轴，AD∥x轴，B（1，0）、C（3，0）。

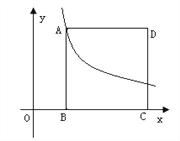
⑴试判断四边形ABCD的形状。

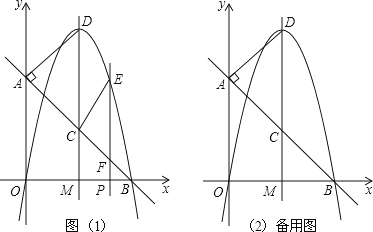
⑵如图若点P是线段BD上一点PE⊥BC于E，M是PD的中点，连EM、AM。

求证：AM=EM

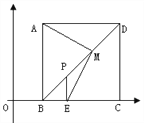
⑶在图中，连结AE交BD于N，则下列两个结论：

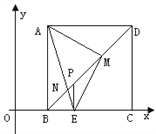
①值不变；②的值不变。其中有且仅有一个是正确的，请选择正确的结论证明并求其值。

Answer 1

【答案】（1）证明见解析（2）证明见解析（3）1

【解析】分析：（1）由AB∥CD∥y轴,AD∥x轴，可得：四边形ABCD为矩形，根据A点函数为得：，从而可证：四边形ABCD为正方形；
（2）作辅助线，延长EM交CD的延长线于G，连AE、AG，由， 可证：△PME≌△DMG，可得： 同理，可证：Rt△ABE≌Rt△ADG，可得： 从而可证：
（3）作辅助线，在图2的AG上截取AH=AN，连DH、MH，由 可证：△ABN≌△ADH， 可得： 同理可证：△AMN≌△AMH，，可得： 故：为定值．

详解：

(1)∵AB∥CD∥y轴,AD∥x轴，

∴四边形ABCD为矩形，

当x=1时，y=AB=2，

∴AB=2，

∵BC=2，

∴AB=BC，

∴四边形ABCD是正方形.

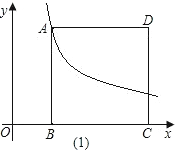
(2)证明：延长EM交CD的延长线于G，连AE、AG，

∵PE∥GC，

∴∠PEM=∠DGM，

又∵∠PME=∠GMD,PM=DM,

∴△PME≌△DMG，

∴EM=MG，PE=GD，

∵PE=BE，

∴BE=GD，

在Rt△ABE与Rt△ADG中，

∴Rt△ABE≌Rt△ADG，

∴AE=AG，∠BAE=∠DAG，

∴

∴

(3)的值不变，值为1.理由如下：

在图2的AG上截取AH=AN，连DH、MH，

∵AB=AD，AN=AH，

由(2)知∠BAN=∠DAH，

∴△ABN≌△ADH，

∴

∴

∴

由(2)知

又AN=AH，AM=AM，

∴△AMN≌△AMH，

∴MN=MH，

∴

即