题目内容
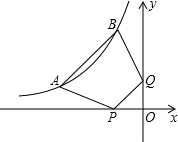
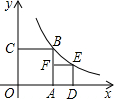
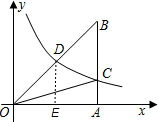
如图，已知双曲线y=
(k＞0)经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为6，则k的值为（ ）
| k |
| x |
| A．1 | B．2 | C．3 | D．4 |
过D点作DE⊥x轴，垂足为E，
由双曲线上点的性质，得S△AOC=S△DOE=
k，
∵DE⊥x轴，AB⊥x轴，
∴DE∥AB，
∴△OAB∽△OED，
又∵OB=2OD，
∴S△OAB=4S△DOE=2k，
由S△OAB-S△OAC=S△OBC，
得2k-
k=6，
解得k=4．
故选D．
由双曲线上点的性质，得S△AOC=S△DOE=
| 1 |
| 2 |
∵DE⊥x轴，AB⊥x轴，
∴DE∥AB，
∴△OAB∽△OED，
又∵OB=2OD，
∴S△OAB=4S△DOE=2k，
由S△OAB-S△OAC=S△OBC，
得2k-
| 1 |
| 2 |
解得k=4．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
，将△OAB绕O点顺时针旋转30°后，恰好A点在双曲线y=
