题目内容
【题目】如图,在平行四边形ABCD中,以A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,延长BA与⊙A相交于点F.若![]() 的长为
的长为![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

【答案】2-![]()
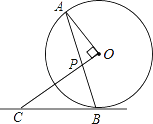
【解析】试题分析:(1)由垂直定义得∠A+∠APO=90°,根据等腰三角形的性质由CP=CB得∠CBP=∠CPB,根据对顶角相等得∠CPB=∠APO,所以∠APO=∠CBP,而∠A=∠OBA,所以∠OBC=∠CBP+∠OBA=∠APO+∠A=90°,然后根据切线的判定定理得到BC是⊙O的切线;
(2)设BC=x,则PC=x,在Rt△OBC中,根据勾股定理得到(![]() )2+x2=(x+1)2,然后解方程即可.
)2+x2=(x+1)2,然后解方程即可.
解:如图所示,∵CD与⊙A相切,
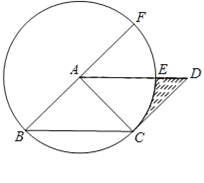
∴CD⊥AC,
在平行四边形ABCD中,
∵AB=DC,AB∥CD,AD∥BC,
∴BA⊥AC,
∵AB=AC
∴∠ACB=∠B=45°,
∵,AD∥BC
∴∠FAE=∠B=45°,∠DAC=∠ACB=45°=∠FAE,
∴![]() =
=![]() ,
,
∴![]() 的长度=
的长度=![]() ,解得R=2,
,解得R=2,
∴S阴影=S△ACD﹣S扇形=![]() ×22﹣
×22﹣![]() =2﹣
=2﹣![]() .
.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量(m3) | 38 | 36 | 34 | 32 | … |
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t