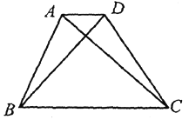
��Ŀ����
����Ŀ����ͼ����A��B�ֱ�������ԭ��O�����࣬��![]() OB+8=OA����A��Ӧ����20.
OB+8=OA����A��Ӧ����20.
��1����B������Ӧ������
��2������P��Q��R�ֱ��B��O��Aͬʱ����������P��Q�������˶����ٶȷֱ�Ϊ2����λ����/�룬4����λ����/�룬��R�����˶����ٶ�Ϊ5����λ����/�룬�����ǵ��˶�ʱ��Ϊt�룬����Rǡ��ΪPQ���е�ʱ����t��ֵ��R����ʾ������
��3����![]() ʱ��BP+
ʱ��BP+![]() AQ��ֵ�Ƿֲ��䣿�����䣬ֱ��д����ֵ�����仯����˵������.
AQ��ֵ�Ƿֲ��䣿�����䣬ֱ��д����ֵ�����仯����˵������.
![]()
���𰸡���1����B��ʾ����Ϊ![]() ����2��t=4��R��ʾ����Ϊ0����3�����䣬��ֵΪ10
����2��t=4��R��ʾ����Ϊ0����3�����䣬��ֵΪ10
��������
��1�����ݵ�A��Ӧ�������OA�ij��ȣ������֪������ͼ�������B����Ӧ������
��2�����ݵ�P��Q��R�ij����㡢�˶��ٶȣ��ɵó������˶�ʱ��Ϊt��ʱ����Q��Ӧ����Ϊ4t����P��Ӧ����Ϊ2t24����R��Ӧ����Ϊ5t��20����ϵ�R��PQ���е㣬���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��3���ֱ��ʾ��BP��AQ��ֵ���������BP+![]() AQ��ֵ���ɽ��
AQ��ֵ���ɽ��
�⣺��1������A��Ӧ������20��
��OA��20��
��![]() OB+8=OA��
OB+8=OA��
��OB��24��
������B��ԭ�����࣬
����B��Ӧ����Ϊ24��
��2�����˶�ʱ��Ϊt��ʱ����Q��Ӧ����Ϊ4t����P��Ӧ����Ϊ2t24����R��Ӧ����Ϊ5t��20��
�����⣬�ã�4t��2t24��2��5t��20����
��ã�t��4��
�𣺵���Rǡ��ΪPQ���е�ʱ��t��ֵΪ4��
��R��Ӧ����Ϊ��![]() ����R��ʾ����Ϊ0.
����R��ʾ����Ϊ0.
��3�����˶�ʱ��Ϊt�룬��![]() ,
,![]() ,
,
��![]() ,
,
��![]() ��ֵ���䣬��ֵΪ10.
��ֵ���䣬��ֵΪ10.

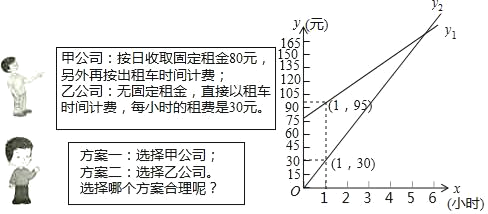
 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij���ɵij�����������������֮��Ĺ�ϵ���±���
�������������/ǧ�� | 0 | 1 | 2 | 3 | 4 | 5 |
���ɵij���/���� | 10 | 10.4 | 10.8 | 11.2 | 11.6 | 12 |
��1��������������������x��ʾ�����ɵij�����y��ʾ����ֱ��д��y��x����Ĺ�ϵʽ��
��2�����������������Ϊ10ǧ��ʱ�����ɵij����Ƕ��٣�
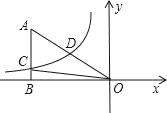
����Ŀ��������һ�����⣺
̽������![]() ��ͼ��������.
��ͼ��������.
С������ѧϰ�����ľ��飬�Ժ���![]() ��ͼ�������ʽ�����̽��.
��ͼ�������ʽ�����̽��.
������С����̽�����̣��벹����ɣ�
��1�����
| �� |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | . . . |
| �� | 3 | 2 |
|
| . . . |
��2�����ݣ�1���еĽ����������������ϵ�л�������![]() ��ͼ��
��ͼ��