��Ŀ����
����Ŀ���Ķ����в��ϣ�
���Ƕ��壺��һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ��������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ��������ξ��Ǻ�г�ı��Σ�����Ķ����ϣ�����������⣺
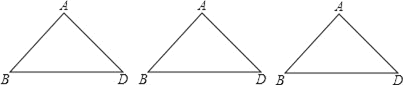
��1�������ĸ��ı���һ���Ǻ�г�ı����� ����
A��ƽ���ı��� B������ C������ D����������
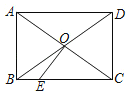
��2�����⣺����г�ı���һ������Գ�ͼ�������� �� ���⣨��������������������
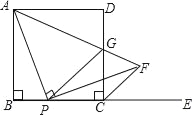
��3����ͼ������Rt��ABD�У���BAD��90��������CΪƽ����һ�㣬ACΪ�ı���ABCD�ĺ�г�ߣ���AB��BC���������ABC�Ķ�����
���𰸡���1�� C ����2���٣���3����ABC�Ķ���Ϊ60����90����150��.
��������
��1���ɺ�г�ı��εĶ��壬���ɵõ������Ǻ�г�ı��Σ�
��2����г�ı��β�һ������Գ�ͼ�Σ��ٳ��������ɣ�
��3�����ȸ������⻭��ͼ�Σ�Ȼ����AC���ı���ABCD�ĺ�г�ߣ����Եó���ACD�ǵ��������Σ���ͼ1��ͼ2��ͼ3����������õȱ������ε����ʣ������ε����ʺ�30����ֱ�����������ʣ����������ABC�Ķ�����
��1�����ݺ�г�ı��ζ��壬ƽ���ı��Σ����Σ��������εĶԽ��߲��ܰ��ı��ηֳ��������������Σ����ε�һ���Խ����ܰ��ı��ηֳ��������������ι���
��ѡC.
��2����г�ı��β�һ������Գ�ͼ�Σ���ͼ��ʾ��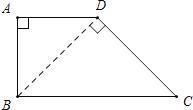
��C=45����ֱ������ABCD�Ǻ�г�ı��Σ���������Գ�ͼ�Σ�
�ʴ�Ϊ���٣�
��3����AC���ı���ABCD�ĺ�г�ߣ���AB=BC��
���ACD�ǵ��������Σ�
���ڵ���Rt��ABD�У�AB=AD��
��AB=AD=BC��
����ͼ1����AD=ACʱ��
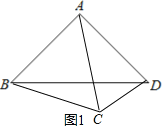
��AB=AC=BC����ACD=��ADC
���ABC����������
���ABC=60����
����ͼ2����DA=DCʱ��
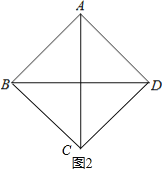
��AB=AD=BC=CD��
�ߡ�BAD=90����
���ı���ABCD�������Σ�
���ABC=90����
����ͼ3����CA=CDʱ������C��CE��AD��E������B��BF��CE��F��
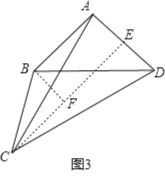
��AC=CD��CE��AD��
��AE=ED����ACE=��DCE��
�ߡ�BAD=��AEF=��BFE=90����
���ı���ABFE�Ǿ��Σ�
��BF=AE��
��AB=AD=BC��
��BF=![]() BC��
BC��
���BCF=30����
��AB=BC��
���ACB=��BAC��
��AB��CE��
���BAC=��ACE��
���ACB=��BAC=![]() ��BCF=15����
��BCF=15����
���ABC=150����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��![]() ��ͨ�ˣ��й���ͨ�������ʷѱ������а���186Ԫʱ���������ֹ��ڲ���0.36Ԫ/�֣�����ҵ��࣬С���İְִ�绰�ѳ����˰��·ѣ��±��dz������ֹ��ڲ�����շѱ���
��ͨ�ˣ��й���ͨ�������ʷѱ������а���186Ԫʱ���������ֹ��ڲ���0.36Ԫ/�֣�����ҵ��࣬С���İְִ�绰�ѳ����˰��·ѣ��±��dz������ֹ��ڲ�����շѱ���
ʱ��/�� | 1 | 2 | 3 | 4 | 5 | �� |
�绰��/Ԫ | 0.36 | 0.72 | 1.08 | 1.44 | 1.80 | �� |
��1���������ӳ������������֮��Ĺ�ϵ���ĸ����Ա�����
��2�������x��ʾ����ʱ�䣬y��ʾ�������ֵĵ绰�ѣ���ôy��x�Ĺ�ϵʽ��ʲô��
��3�������绰����![]() ���ӣ���ึ���ٵ绰�ѣ�
���ӣ���ึ���ٵ绰�ѣ�
��4��ij�δ�绰�ķ��ó���������![]() Ԫ����ôС���İְִ�绰���������ӣ�
Ԫ����ôС���İְִ�绰���������ӣ�