题目内容
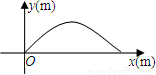
一次高尔夫球的比赛中,在O处击球,球的飞行路线满足抛物线y=-| 1 |
| 5 |
| 8 |
| 5 |
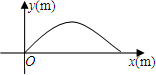 球的飞行高度,x(m)是球飞出的水平距离.
球的飞行高度,x(m)是球飞出的水平距离.(1)请求出当球水平飞行距离为多少米时,球的高度达到最大,并求出最大高度.
(2)这次击球,球飞行的最大水平距离是多少?
分析:(1)把y=-
x2+
x配成抛物线的顶点式,得y=-
(x-4)2+
,然后根据二次函数的最值问题进行回答即可;
(2)当高度y=0时,球飞行的水平距离最大.对于y=-
x2+
x,令y=0,得到关于x的方程,解方程即可.
| 1 |
| 5 |
| 8 |
| 5 |
| 1 |
| 5 |
| 16 |
| 5 |
(2)当高度y=0时,球飞行的水平距离最大.对于y=-
| 1 |
| 5 |
| 8 |
| 5 |
解答:解:(1)∵y=-
x2+
x
=-
(x-4)2+
,
∴当x=4时,y有最大值为
.
所以当球水平飞行距离为4米时,球的高度达到最大,最大高度为
米;
(2)令y=0,
∴-
x2+
x=0,解得x1=0,x2=8,
所以这次击球,球飞行的最大水平距离是8米.
| 1 |
| 5 |
| 8 |
| 5 |
=-
| 1 |
| 5 |
| 16 |
| 5 |
∴当x=4时,y有最大值为
| 16 |
| 5 |
所以当球水平飞行距离为4米时,球的高度达到最大,最大高度为
| 16 |
| 5 |
(2)令y=0,
∴-
| 1 |
| 5 |
| 8 |
| 5 |
所以这次击球,球飞行的最大水平距离是8米.
点评:本题考查了二次函数的应用:先把二次函数关系式变形成顶点式:y=a(x-k)2+h,当a<0,x=k时,y有最大值h;当a>0,x=k时,y有最小值h.

练习册系列答案
相关题目
 30°,O、A两点相距
30°,O、A两点相距 30°,O、A两点相距
30°,O、A两点相距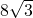 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题: x2+
x2+ x,其中y(m)是
x,其中y(m)是 球的飞行高度,x(m)是球飞出的水平距离.
球的飞行高度,x(m)是球飞出的水平距离. x2+
x2+ x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离.
x,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离.