题目内容
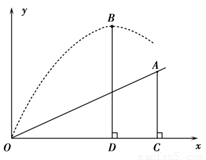
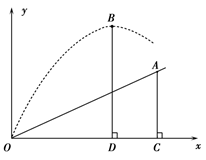
小明在一次高尔夫球比赛中,从山坡下的O点打出一记球向山坡上的球洞A点飞去,球的飞行路线为抛物线.如果不考虑空气阻力,当球飞行的水平距离为9米时,球达到最大水平高度为12米.已知山坡OA与水平方向的夹角为 30°,O、A两点相距
30°,O、A两点相距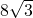 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
(1)求出点A的坐标;
(2)判断小明这一杆能否把高尔夫球从O点直接打入球洞A点,并说明理由.
 解:(1)在Rt△AOC中,
解:(1)在Rt△AOC中,∵∠AOC=30°,OA=8
 ,
,∴AC=OA•sin30°=8
 ×
× =4
=4 ,
,OC=OA•cos30°=8
 ×
× =12,
=12,∴点A的坐标为(12,4
 );
);(2)小明这一杆不能把高尔夫球从O点直接打入球洞A点.
∵顶点B的坐标是(9,12),∴设抛物线的解析式为y=a(x-9)2+12,
∵点O的坐标是(0,0)
∴把点O的坐标代入得:
0=a(0-9)2+12,
解得a=-
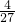 ,
,抛物线的解析式为y=-
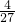 (x-9)2+12
(x-9)2+12即y=-
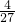 x2+
x2+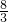 x,
x,当x=12时,y=
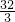 ≠4
≠4 ,
,所以小明这一杆不能把高尔夫球从O点直接打入球洞A点.
分析:(1)已知OA与水平方向OC的夹角为30°,OA=8
 米,解直角三角形可求点A的坐标;
米,解直角三角形可求点A的坐标;(2)小明这一杆不能把高尔夫球从O点直接打入球洞A点,分析题意可知,抛物线的顶点坐标为(9,12),经过原点(0,0),设顶点式可求抛物线的解析式,把点A的横坐标x=12代入抛物线解析式,看函数值与点A的纵坐标是否相符.
点评:本题考查了点的坐标求法,二次函数解析式的确定方法,及点的坐标与函数解析式的关系.

练习册系列答案
相关题目
 30°,O、A两点相距
30°,O、A两点相距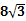 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
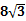 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题:
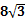 米.请利用下面所给的平面直角坐标系探索下列问题:
米.请利用下面所给的平面直角坐标系探索下列问题: