题目内容

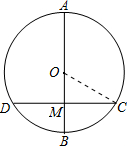
如图，⊙O的直径AB垂直弦CD于M，且M是半径OB的中点，CD=8cm，求直径AB的长．
连接OC，
∵直径AB⊥CD，
∴CM=DM=
1
2
CD=4cm，（2分）
∵M是OB的中点，
∴OM=
1
2
OB=
1
2
OC
由勾股定理得：
OC2=OM2+CM2
∴OC2=
1
4
OC2+42，
∴OC=
8
3
3
cm（3分）
∴直径AB的长=
16
3
3
cm．（1分）
练习册系列答案
相关题目
如图，△ABC中A（-2，3），B（-3，1），C（-1，2）．
（1）将△ABC向右平移4个单位长度，画出平移后的△A1B1C1；
（2）画出△ABC关于x轴对称的△A2B2C2；
（3）将△ABC绕原点O旋转180°，画出旋转后的△A3B3C3；
（4）在△A1B1C1、△A2B2C2、△A3B3C3中，△______与△______成轴对称，对称轴是______；△______与△______成中心对称，对称中心的坐标是______．
⊙O的半径r=1，弦AC=
2
，弦AB=
3
，则∠BAC的度数是______．
如图，一车轱辘⊙O抵住高为10cm的路沿AB，此时发现轮胎与地面的接触点C与路沿下端B的距离恰好为30cm（∠ABC=90°），请你利用已学的知识，求出车轱辘的直径．
如图，⊙O的弦AB垂直于直径MN，C为垂足，若OA=5cm，下面四个结论中可能成立的是（　　）
A．AB=12cmB．OC=6cmC．MN=8cmD．OC=2.5cm
如图，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．若EB=8cm，CD=24cm，求⊙O的直径．
过⊙O内一点P的最长弦长为10cm，最短弦长为6cm，则OP的长为______cm．
如图，AB是⊙O直径，OB=6，弦CD=10，则弦心距OP的长为（　　）
A．8B．4C．
26
D．
11
如图，⊙O的半径是10cm，点A在⊙O上，线段AC交⊙O于点B，AC=23cm，AB=12cm，点P在线段AC上，设AP=x（cm），OP=y（cm）．
（1）求y关于x的函数关系式，及x的取值范围；
（2）当x=4、14时，求y的值；
（3）当y=8时，求x的值；
（4）当x为何值时，10≤y≤17？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网