题目内容
【题目】如图,在矩形ABCD中,E是AD上一点,AB=8,BE=BC=10,动点P在线段BE上(与点B、E不重合),点Q在BC的延长线上,PE=CQ,PQ交EC于点F,PG∥BQ交EC于点G,设PE=x.
(1)求证:△PFG≌△QFC
(2)连结DG.当x为何值时,四边形PGDE是菱形,请说明理由;
【答案】
(1)证明:∵BC=BE,∴∠BCE=∠PEC,
∵PG∥BQ,
∴∠BCE=∠PGE,∠Q=∠FPG,∠QCF=∠PGF,
∴∠PGE=∠PEC,
∴PE=PG,
∵PE=CQ,
∴PG=CQ,
∴△PFG≌△QFC (ASA).
(2)解:结论:当x=4时,四边形PGDE是菱形.
理由如下:连结DG
∵四边形ABCD是矩形,
∴AD∥BC,
AB=CD=8,AD=BC=BE=10,
在Rt△ABE中,AE= ![]() ,
,
∴DE=AD﹣AE=10﹣6=4,
由(1)知PG=PE=x=4,
∴PG=DE,
∵PG∥BQ,AD∥BC,
∴PG∥DE,
∴四边形PGDE是平行四边形,
∵PG=PE=4,
∴四边形PGDE是菱形.
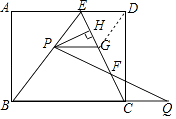
;(3)作PH⊥EC于点H.探究:
①点P在运动过程中,线段HF的长度是否发生变化?若变化,说明理由;若不变,求HF的长度;
②当x为何值时,△PHF与△BAE相似.
解:①不变化.
理由:在Rt△ABE中,CE= ![]() ,
,
∵PG=PE,PH⊥EC,
∴EH=HG= ![]() EG(等腰三角形“三线合一”),
EG(等腰三角形“三线合一”),
∵△PFG≌△QFC,
∴CF=GF= ![]() CG,
CG,
∴HF=HG+FG= ![]() EG+
EG+ ![]() CG=
CG= ![]() CE=
CE= ![]() ,
,
②∵PG∥DE,
∴∠DEC=∠PGH,
在Rt△PGH中,PH=PG×sin∠PGH=x×sin∠DEC=x× ![]() =x×
=x× ![]() =
= ![]() ,
,
分两种情况讨论:
(Ⅰ)若△PHF∽△EAB,则 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() 时,△PHF∽△BAE.
时,△PHF∽△BAE.
(II)若△PHF∽△BAE,则 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() 或
或 ![]() 时,△PHF与△BAE相似.
时,△PHF与△BAE相似.
【解析】(1)只要证明PG=CQ,即可根据AAS或ASA证明;(2)结论:当x=4时,四边形PGDE是菱形.首先证明四边形PGDE是平行四边形,由PG=PE=4,即可推出四边形PGDE是菱形;(3)①不变化.可以证明:HF=HG+FG= ![]() EG+
EG+ ![]() CG=
CG= ![]() CE=
CE= ![]() ;②分两种情形讨论(Ⅰ)若△PHF∽△EAB,则
;②分两种情形讨论(Ⅰ)若△PHF∽△EAB,则 ![]() ,(II)若△PHF∽△BAE,则
,(II)若△PHF∽△BAE,则 ![]() ,分别列出方程即可解决问题;
,分别列出方程即可解决问题;
【考点精析】根据题目的已知条件,利用相似三角形的应用的相关知识可以得到问题的答案,需要掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.

【题目】一次期中考试中A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:
A | B | C | D | E | 平均分 | 标准差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
【1】求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
【2】为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是标准分=(个人成绩-平均成绩)÷成绩标准差. 从标准分看,标准分大的考试成绩更好,请问A同学在本次考试中,数学与英语哪个学科考得更好.