Question

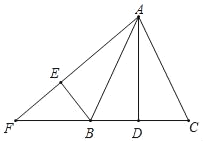
【题目】如图，△ABC中，AB＝AC，D是BC边的中点，点E与点D关于AB对称，连接AE、BE，分别延长AE、CB交于点F，若∠F＝48°，则∠C的度数是（　　）

A. 21°B. 52°C. 69°D. 74°

Answer 1

【答案】C

【解析】

由等腰三角形三线合一可知AD⊥BC，又易知△ABD≌△ABE，所以∠AEB=∠ADB=90°，所以∠EBF=90°-48°=42°，得到∠EBC=180°-42°=138°，得到∠ABC=69°，可得∠C=69°

∵AB=AC，D是AC中点

∴AD⊥BC，∠ABC=∠C

∵B点和E点关于AB对称

∴△ABD≌△ABE

∴∠AEB=∠ADB=90°，∠ABE=∠ABD

∵∠F=48°

∴∠EBF=∠AEB -∠F =90°-48°=42°

∴∠ABC=（180°-∠FBE）=69°

∴∠C=∠ABC=69°

故选C