题目内容
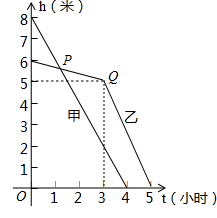 甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).
甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).(1)在哪一段时间内,乙池的放水速度快于甲池的放水速度?
(2)求点P的坐标,由此得到什么结论?
(3)当一个池中的水先放完时,另一个池中水面的高度是多少米?
分析:(1)根据图象先求出甲与乙的放水速度,再根据图象即可得出结论;
(2)甲池中水面高度h(米)与时间t(小时)的函数关系为h=-2t+8.当0≤t≤3时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
t+6.两者相等即可求出p点坐标;
(3)由图知,甲池中的水4小时放完,把t=4代入乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
t+
,
即可求解;
(2)甲池中水面高度h(米)与时间t(小时)的函数关系为h=-2t+8.当0≤t≤3时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
| 1 |
| 3 |
(3)由图知,甲池中的水4小时放完,把t=4代入乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
| 5 |
| 2 |
| 25 |
| 2 |
即可求解;
解答:解:(1)由图知,甲池的放水速度为
=2(米/小时).
当0≤t≤3时,乙池的放水速度为
(米/小时);
当3<t≤5时,乙池的放水速度为
(米/小时).
因为
<2,2<
,
所以3<t≤5时,乙池的放水速度快于甲池的放水速度;
(2)甲池中水面高度h(米)与时间t(小时)的函数关系为h=-2t+8.
当0≤t≤3时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
t+6.
由
解得
所以P(
,
),即P(1.2,5.6).
由此说明,当t=1.2小时时,两池中水面的高度相等;
(3)由图知,甲池中的水4小时放完.
当3<t≤5时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
t+
.
当t=4时,h=
,即h=2.5.
所以当甲池中的水先放完时,乙池中水面的高度是2.5米.
| 8 |
| 4 |
当0≤t≤3时,乙池的放水速度为
| 1 |
| 3 |
当3<t≤5时,乙池的放水速度为
| 5 |
| 2 |
因为
| 1 |
| 3 |
| 5 |
| 2 |
所以3<t≤5时,乙池的放水速度快于甲池的放水速度;
(2)甲池中水面高度h(米)与时间t(小时)的函数关系为h=-2t+8.
当0≤t≤3时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
| 1 |
| 3 |
由
|
|
| 6 |
| 5 |
| 28 |
| 5 |
由此说明,当t=1.2小时时,两池中水面的高度相等;
(3)由图知,甲池中的水4小时放完.
当3<t≤5时,乙池中水面高度h(米)与时间t(小时)的函数关系为h=-
| 5 |
| 2 |
| 25 |
| 2 |
当t=4时,h=
| 5 |
| 2 |
所以当甲池中的水先放完时,乙池中水面的高度是2.5米.
点评:本题考查了一次函数的应用,难度较大,关键是掌握根据图象获取信息的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (m3)与放水时间x(h)的关系如图所示.已知乙水池容量比甲水池容量少5m3.请根据下图所提供的信息解答下列问题:
(m3)与放水时间x(h)的关系如图所示.已知乙水池容量比甲水池容量少5m3.请根据下图所提供的信息解答下列问题: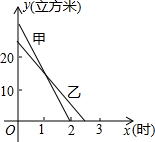 、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.
、乙两蓄水池中剩余水量y(立方米)与放水时间x(小时)之间的关系如图所示,已知y乙=-10x+25.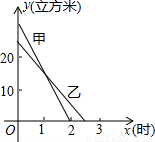
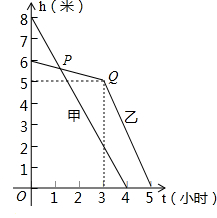 甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).
甲、乙两个水池同时放水,其水面高度(水面离池底的距离)h(米)与时间t(小时)之间的关系如图所示(甲、乙两个水池底面相同).