题目内容
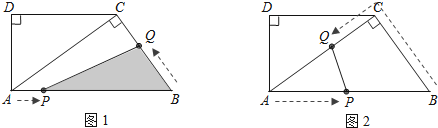
【题目】如图，Rt△CEF中，∠C=90°，∠CEF, ∠CFE外角平分线交于点A，过点A分别作直线CE、CF的垂线，B、D为垂足.
(1)求证:四边形ABCD是正方形，
(2)已知AB的长为6，求(BE+6)(DF+6)的值，
(3)借助于上面问题的解题思路，解决下列问题:若三角形PQR中，∠QPR=45°，一条高是PH，长度为6,QH=2，则HR= .
【答案】（1）见解析；（2）72；（3）3.
【解析】
（1）根据三个角是直角的四边形先证得四边形ABCD是矩形，再过点A作AG⊥EF于点G，根据角平分线的性质得出AB=AG= AD，问题即得解决；
（2）如图1，通过两次运用HL可证得EF=BE+DF，再设BE=x，DF=y，在Rt△CEF中，根据勾股定理得出关于x、y的等式，再整体代入
展开整理后的式子即可得到答案；
（3）如图3，作△PRH关于PR对称的△PRN，作△PQH关于PQ对称的△PQM，NR和MQ的延长线交于点K，先根据邻边相等的矩形是正方形证明四边形PNKM是正方形，再根据（2）的结论即可求出结果.
解：（1）证明：∵AD⊥CD，AB⊥CB，∠C=90°，
∴四边形ABCD是矩形，
如图1，过点A作AG⊥EF于点G，
∵AF平分∠DFE，AD⊥CD，
∴AG=AD，
同理可得：AG=AB，
∴AB=AD.
∴矩形ABCD是正方形.
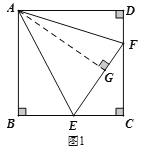
（2）在Rt△ADF和Rt△AGF中，
∴Rt△ADF≌Rt△AGF（HL）.
∴DF=GF，
同理可得BE=GE.
∴EF=GE+GF=BE+DF.
设BE=EG=x，DF=FG=y，则CE=6－x，CF=6－y，如图2：
在Rt△CEF中，根据勾股定理得：
，即
，整理得：
.
∴
.
（3）如图3，作△PRH关于PR对称的△PRN，作△PQH关于PQ对称的△PQM，NR和MQ的延长线交于点K，则PN=PH=6，PM=PH=6，∠2=∠1，∠4=∠3，∠N=∠PHR=90°，∠M=∠PHQ=90°，MQ=HQ=2，NR=HR，
∴PN=PM=6，
∵∠1+∠3=45°，
∴∠1+∠2+∠3+∠4=90°，即∠NPM=90°，
∴四边形PNKM是正方形.
∵RQ=RH+HQ=NR+QM，
∴由（2）题的结论知：
，
即
，解得
，即HR=3.
故答案为3.
