题目内容
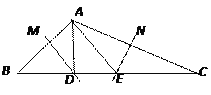
【题目】如图,在ABCD中,AD=2AB,F是AD的中点,E是AB上一点,连接CF、EF,且CF=EF.
(1)若∠CFD=55°,求∠BCD的度数;
(2)求证:∠EFC=2∠CFD;
(3)求证:CE⊥AB.
【答案】(1)110°;(2)见解析;(3)见解析
【解析】
试题分析:(1)根据平行四边形的性质得出AD∥BC,根据平行线的性质得出∠BCF=∠CFD=55°,求出DF=DC,根据等腰三角形的性质得出∠DCF=∠CFD=55°,即可求出答案;
(2)延长EF和CD交于M,根据平行四边形的性质得出AB∥CD,根据平行线的性质得出∠A=∠FDM,证△EAF≌△MDF,推出EF=MF,求出CF=MF,求出∠M=∠FCD=∠CFD,根据三角形的外角性质求出即可;
(3)求出∠ECD=90°,根据平行线的性质得出∠BEC=∠ECD,即可得出答案.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,
∵∠CFD=55°,
∴∠BCF=∠CFD=55°,
∵在ABCD中,AD=2AB,
∴AD=2DC,
∵F为AD的中点,
∴AF=DF,AD=2DF,
∴DF=DC,
∴∠DCF=∠CFD=55°,
∴∠BCD=∠BCF+∠DCF=55°+55°=110°;
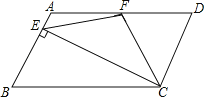
(2)证明:延长EF和CD交于M,
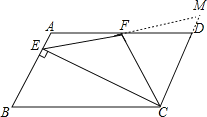
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠FDM,
在△EAF和△MDF中,
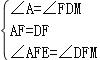 ,
,
∴△EAF≌△MDF(ASA),
∴EF=MF,
∵EF=CF,
∴CF=MF,
∴∠FCD=∠M,
∵由(1)知:∠DFC=∠FCD,
∴∠M=∠FCD=∠CFD,
∵∠EFC=∠M+∠FCD=2∠CFD;
(3)解:∵EF=FM=CF,
∴∠ECM=90°,
∵AB∥CD,
∴∠BEC=∠ECM=90°,
∴CE⊥AB.

 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案【题目】一张长方形的餐桌可以坐6个人,按照下图的方式摆放餐桌和椅子:

(1)观察表中数据规律填表:
餐桌张数 | 1 | 2 | 3 | 4 | …n |
可坐人数 | 6 | 8 | 10 |
(2)一家酒楼,按上图的方式拼桌,要使拼成的一张大餐桌刚好能坐160人,请问需几张餐桌拼成一张大餐桌?
(3)若酒店有240人来就餐,哪种拼桌的方式更好?最少要用多少张餐桌?