题目内容
【题目】如图(1),在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A坐标(6,0),点B在y轴上,点C在第三象限角平分线上,动点P、Q同时从点O出发,点P以1cm/s 的速度沿O→A→B匀速运动到终点B;点Q沿O→C→B→A运动到终点A,点Q在线段OC、CB、BA上分别作匀速运动,速度分别为V1cm/s、V2cm/s、V3cm/s.设点P运动的时间为t(s),△OPQ的面积为S(cm2),已知S与t之间的部分函数关系如图(2)中的曲线段OE、曲线段EF和线段FG所示.
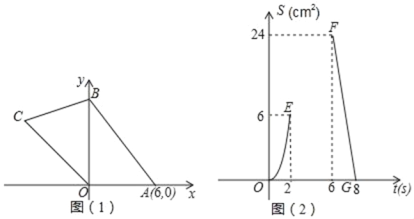
(1)V1= ,V2= ;
(2)求曲线段EF的解析式;
(3)补全函数图象(请标注必要的数据);
(4)当点P、Q在运动过程中是否存在这样的t,使得直线PQ把四边形OABC的面积分成11:13两部分,若存在直接写出t的值;若不存在,请说明理由.
【答案】(1)3![]() ,
,![]() ;(2) S=
;(2) S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6;(3)见解析;(4)见解析.
t(2<t≤6;(3)见解析;(4)见解析.
【解析】
(1)观察图象可知,t=2时,点Q运动到点C位置,t=6时,点Q运动到点B位置.如图1中,作CE⊥x轴于E,CF⊥OB于F.利用图中信息,求出点C、B坐标即可解决问题.
(2)如图1中,当点Q在线段BC上时,作QN⊥OE于N,交CF于M.由QM∥BF,可得![]() =
=![]() ,推出
,推出![]() =
=![]() ,可得QM=
,可得QM=![]() ,QN=
,QN=![]() ,可得S=
,可得S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6).
t(2<t≤6).
(3)利用描点法即可解决问题;
(4)分两种情形构建方程即可解决问题;
解:(1)观察图象可知,t=2时,点Q运动到点C位置,t=6时,点Q运动到点B位置.
如图1中,作CE⊥x轴于E,CF⊥OB于F.
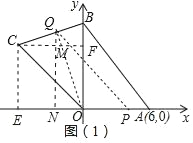
由题意6=![]() ×2×CE,
×2×CE,
∴CE=6,
∵∠COE=45°,
∴CE=OE=OF=CF=6,OC=6![]() ,
,
∴V1=![]() =3
=3![]() cm/s,
cm/s,
在Rt△CBF中,BC=![]() =2
=2![]() ,
,
∴V2=![]() =
=![]() cm/s,
cm/s,
故答案为3![]() ,
,![]() .
.
(2)如图1中,当点Q在线段BC上时,作QN⊥OE于N,交CF于M.
∵QM∥BF,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴QM=![]() ,QN=
,QN=![]() ,
,
∴S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6).
t(2<t≤6).
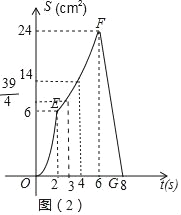
(3)在S=![]() t
t![]() =
=![]() t2+
t2+![]() t(2<t≤6)上取点(3,
t(2<t≤6)上取点(3,![]() ),(4,14),
),(4,14),
函数图象如图所示:
(4)如图3中,由题意满足条件的点Q在线段BC上,点P在线段OA上.
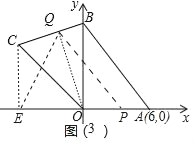
∵四边形AOCB的面积为48,
∴当四边形POCQ的面积=22或26时,满足条件,
∵S四边形POCQ=S△ECQ+S△PEQ,
<>则有:解得t=﹣17+![]() 或﹣17+3
或﹣17+3![]() (负根已经舍弃).
(负根已经舍弃).
∴t=﹣17+![]() 或﹣17+3
或﹣17+3![]() s时,直线PQ把四边形OABC的面积分成11:13两部分.
s时,直线PQ把四边形OABC的面积分成11:13两部分.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案







