题目内容
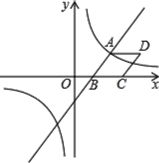
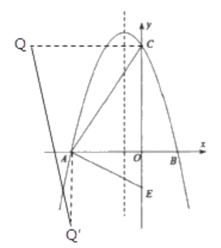
【题目】如图所示,在平面直角坐标系中,二次函数y=ax2+bx+6(a≠0)交x轴于A(﹣4,0),B(2,0),在y轴上有一点E(0,﹣2),连接AE.
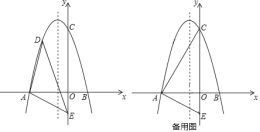
(1)求二次函数的表达式;
(2)点D是第二象限内的抛物线上一动点.
①求△ADE面积最大值并写出此时点D的坐标;
②若tan∠AED=![]() ,求此时点D坐标;
,求此时点D坐标;
(3)连接AC,点P是线段CA上的动点,连接OP,把线段PO绕着点P顺时针旋转90°至PQ,点Q是点O的对应点.当动点P从点C运动到点A,则动点Q所经过的路径长等于 (直接写出答案).
【答案】(1)y=﹣![]() x2﹣
x2﹣![]() x+6;(2)①当m=﹣
x+6;(2)①当m=﹣![]() 时,S△ADE的面积最大,最大值为
时,S△ADE的面积最大,最大值为![]() ;点D点坐标为(
;点D点坐标为(![]() ,
,![]() );②D(
);②D(![]() ,
,![]() );(3)2
);(3)2![]() .
.
【解析】
(1)把点A(﹣4,0),B(2,0)代入y=ax2+bx+6的解析式即可得解;
(2)①由A、E两点坐标得出直线AE解析式,设点D坐标为(m,﹣![]() m2﹣
m2﹣![]() m+6,过点D作DK⊥y轴交于点K,然后构建S△ADE面积与m的二次函数,即可得出△ADE面积最大值和点D的坐标;
m+6,过点D作DK⊥y轴交于点K,然后构建S△ADE面积与m的二次函数,即可得出△ADE面积最大值和点D的坐标;
②过点A作AN⊥DE,DE与x轴交于点F,通过证明Rt△AFN∽Rt△EFO,得出![]() ,得到点F的坐标,进而得出直线EF的解析式,联立直线和二次函数,得出点D的坐标即可;
,得到点F的坐标,进而得出直线EF的解析式,联立直线和二次函数,得出点D的坐标即可;
(3)根据题意,当P点在A点时,![]() (﹣4,﹣4),当P点在C点时,Q(﹣6,6),动点Q所经过的路径是线段Q
(﹣4,﹣4),当P点在C点时,Q(﹣6,6),动点Q所经过的路径是线段Q![]() ,求出两点之间的距离即可得解.
,求出两点之间的距离即可得解.
(1)将A(﹣4,0),B(2,0)代入y=ax2+bx+6(a≠0),
![]() ,
,
可得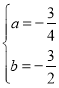 ,
,
∴y=﹣![]() x2﹣
x2﹣![]() x+6,
x+6,
故答案为:y=﹣![]() x2﹣
x2﹣![]() x+6;
x+6;
(2)①∵A(﹣4,0),E(0,﹣2),
设D(m,﹣![]() m2﹣
m2﹣![]() m+6),
m+6),
过点D作DK⊥y轴交于点K,
K(0,﹣![]() m2﹣
m2﹣![]() m+6),
m+6),
S△ADE=S梯形DKOA+S△AOE﹣S△KED
=![]() ×(KD+AO)×OK+
×(KD+AO)×OK+![]() ×AO×OE﹣
×AO×OE﹣![]() ×KD×KE
×KD×KE
=![]() (﹣m+4)×(﹣
(﹣m+4)×(﹣![]() m2﹣
m2﹣![]() m+6)+
m+6)+![]() ×4×2﹣
×4×2﹣![]() ×(﹣m)×(2﹣
×(﹣m)×(2﹣![]() m2﹣
m2﹣![]() m+6)
m+6)
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
当m=﹣![]() 时,S△ADE的面积最大,最大值为
时,S△ADE的面积最大,最大值为![]() ,点D点坐标为(
,点D点坐标为(![]() ,
,![]() ),
),
故答案为: ![]() ;(
;(![]() ,
,![]() );
);
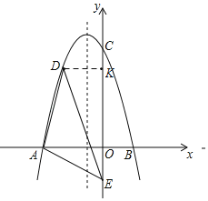
②过点A作AN⊥DE,DE与x轴交于点F,
∵tan∠AED=![]() ,
,
∴AN=![]() ,NE=3
,NE=3![]() ,
,
Rt△AFN∽Rt△EFO,
∴![]() ,
,
∵EF2=OF2+4,
∴NF=3![]() ﹣EF,
﹣EF,
∴![]() =
=![]() ,
,
∴OF=2,
∴F(﹣2,0),
∴EF直线解析式为y=﹣x﹣2,
∴﹣x﹣2=﹣![]() x2﹣
x2﹣![]() x+6时,x=
x+6时,x=![]() ,
,
∴D(![]() ,
,![]() ),
),
故答案为:D(![]() ,
,![]() );
);
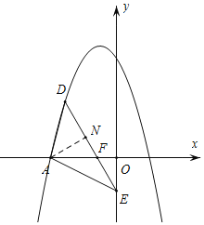
(3)∵Q点随P点运动而运动,P点在线段AC上运动,
∴Q点的运动轨迹是线段,
当P点在A点时,![]() (﹣4,﹣4),
(﹣4,﹣4),
当P点在C点时,Q(﹣6,6),
∴Q点的轨迹长为Q![]() =
=![]() =2
=2![]() ,
,
故答案为:2![]() .
.

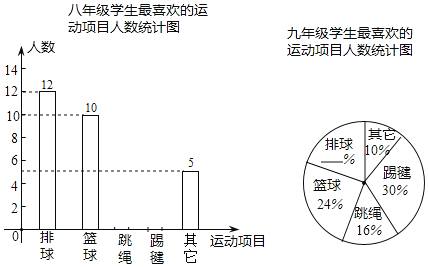
【题目】通辽市某中学为了了解学生“大课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 |
| 6 |
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取了多少人?
(2)补全统计表和统计图.
(3)该校有学生1800人,学校想对“最喜欢踢毽子”的学生每4人提供一个毽子,学校现有124个毽子,能否够用?请说明理由.