��Ŀ����
����Ŀ��һ�����εij�Ϊa����Ϊb(a��0��b��0)������ε����Ϊab.����ʽxy(x��0��y��0)���Կ����DZ߳�Ϊx��y�ľ��ε����.���ǿ����ɴ˽�һԪ���η��̣�x2+x��6��0(x��0).����������£�
�ٷ��̱���Ϊx(x+1)��6.
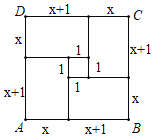
�ڻ��ĸ��߳�Ϊx+1��x�ľ�����ͼ���ã�
���������ϵ��ⷽ��.
��SABCD��(x+x+1)2����SABCD��4x(x+1)+12.
��(x+x+1)2��4x(x+1)+1����x(x+1)��6��
��(2x+1)2��25��
��x��0��
��x��2.
�����������������x�Ķ��η���x2+mx��n��0�Ľ�(x��0��m��0��n��0).(Ҫ����ʾ��ͼ����ע����߶εij��ȣ�д�����ⲽ��)
���𰸡���ͼ��������x��![]() (
(![]() ��m)(m��0��n��0).
��m)(m��0��n��0).
��������
������֪��һԪ���η��̵ľ�����̼������.
�⣺�ٷ��̱���Ϊx(x+m)��n��
�ڻ��ĸ��߳�Ϊx+m��x�ľ�����ͼ���ã�
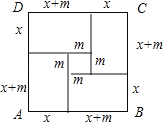
���������ϵ��ⷽ��.
��SABCD��(x+x+m)2����SABCD��4x(x+m)+m2.
��(x+x+m)2��4x(x+m)+m2����x(x+m)��n��
��(2x+m)2��4n+m2����x��0����x��![]() (
(![]() ��m)(m��0��n��0).
��m)(m��0��n��0).

��ϰ��ϵ�д�
�����Ŀ






