题目内容
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的顶点
的顶点![]() 在
在![]() 轴上,且
轴上,且![]() ,则直线
,则直线![]() 的解析式是_____________.
的解析式是_____________.

【答案】![]()
【解析】
根据A(-3,0),B (2,b),得到OA=3,OE=2,易证得![]() ,得到DF=AO=3,OD=AE=CF=5,即可求得点C、D的坐标,从而求得直线
,得到DF=AO=3,OD=AE=CF=5,即可求得点C、D的坐标,从而求得直线![]() 的解析式.
的解析式.
作CF⊥![]() 轴于F,BE⊥
轴于F,BE⊥![]() 轴于E,
轴于E,
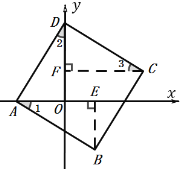
∵A(-3,0),B (2,b),
∴OA=3,OE=2,
∴AE= OA+OE =5,
∵四边形ABCD是正方形,
∴AB=AD=CD,∠BAD=∠ADC=90![]() ,
,
∵∠1+∠DAO=90![]() ,∠2+∠DAO=90
,∠2+∠DAO=90![]() ,∠2+∠CDF=90
,∠2+∠CDF=90![]() ,∠3+∠CDF=90
,∠3+∠CDF=90![]() ,
,
∴∠1=∠2=∠3,
∴![]() ,
,
∴DF=AO=3,OD=AE=CF=5,
∴OF= OD- DF=2,
∴点C的坐标为(5,2),点D的坐标为(0,5),
设直线CD的解析式为![]() ,
,
把点C的坐标为(5,2)代入得:![]() ,
,
解得:![]() ,
,
∴直线CD的解析式为![]() ,
,
故答案为:![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目