题目内容
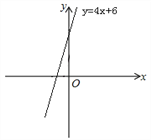
【题目】如图，点M是直线y=4x+6上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使△MNP为等腰直角三角形，请写出符合条件的点P的坐标___．
【答案】(0,1.2)、(0,0)、(0,-2)、(0,1)
【解析】试题解析：当M运动到（-1.2，1.2）时，ON=1.2，MN=1.2，
∵MN⊥x轴，所以由ON=MN可知，（0，0）和（0，1.2）就是符合条件的两个P点；
又∵当M运动到第三象限时，要MN=MP，且PM⊥MN，
设点M（x，4x+6），则有-x=-（4x+6），
解得x=-2，所以点P坐标为（0，-2）．
当点M′在第二象限，M′N′为斜边时，这时N′P=M′P，∠M′N′P=45°，
设点M′（x，4x+6），则OP=ON′，而OP=
M′N′，
∴有-x=
（4x+6），
解得x=-1，这时点P的坐标为（0，1）．
综上，符合条件的点P坐标是（0，1.2），（0，0），（0，-2），（0，1）．
故答案为：（0，1.2），（0，0），（0，-2），（0，1）．
【题目】泉州市某校准备组织教师、学生、家长到福州进行参观学习活动，旅行社代办购买动车票，动车票价格如下表所示：
运行区间 | 大人票价 | 学生票 | ||
出发站 | 终点站 | 一等座 | 二等座 | 二等座 |
泉州 | 福州 | 61.5（元） | 50.5（元） | 38（元） |
根据报名总人数，若所有人员都买一等座的动车票，则共需13530元，若都买二等座动车票（学生全部按表中的“学生票二等座”购买），则共需8860元；已知家长的人数是教师的人数的3倍。
（1）报名参加活动的总人数为___________人；
（2）求参加活动的教师与学生的人数；
（3）如果买到a张成人二等座票，且学生全部按表中的“学生票二等座”购买，其余的买一等座票，但个别家长因临时不参加活动退票，退票人数刚好是所买一等座票数的
，已知退票的是一等座票，退票收取票价10%的退票费，最终买票的总费用为8859.3元，求a的值。
