Question

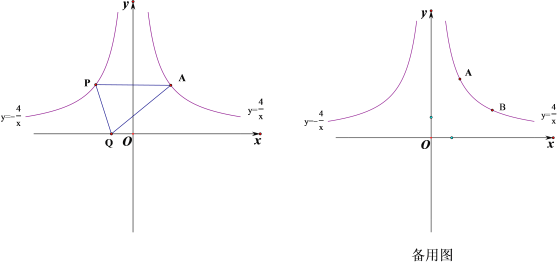
【题目】平面直角坐标系xOy中，已知函数y1=（x＞0）与y2=﹣（x＜0）的图象如图所示，点A、B是函数y1=（x＞0）图象上的两点，点P是y2=﹣（x＜0）的图象上的一点，且AP∥x轴，点Q是x轴上一点，设点A、B的横坐标分别为m、n（m≠n）．

（1）求△APQ的面积；

（2）若△APQ是等腰直角三角形，求点Q的坐标；

（3）若△OAB是以AB为底的等腰三角形，求mn的值．

Answer 1

【答案】（1）S=4（2）（3）mn=4

【解析】试题分析：（1）由点A的横坐标为m，则A（m, ）,P(-m, ),过点P、A、Q分别作PM x轴交x轴于点M，PN x轴交x轴于点N，QR AP交AP轴于点R，可得出S矩形PMNA＝8，由四边形PMQR和四边形ARQN是矩形可得：S△PQM＝S△PRQ，S△ANQ＝S△ARQ，所以S△APQ＝S△PRQ+ S△ARQ＝ S矩形PMNA；(2)分情况讨论，当PQx轴时，求得，当PQ＝AQ时；(3)由OA＝OB，解得mn=4.

试题解析：

（1）过点P、A、Q分别作PM x轴交x轴于点M，PN x轴交x轴于点N，QR AP轴交AP轴于点R，则四边形APMN、四边形PMQR、四边形ARQN是矩形，如图所示：

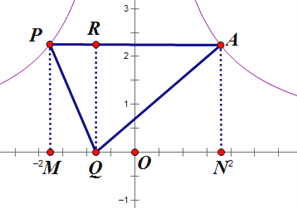
∵点A的横坐标为m,且在函数上，AP∥x轴,且点P在函数上，

∴点A（m, ）,点P（－m, ）,

∴MN=m-(-m)=2m,PM=,

∴S矩形PMNA＝2m╳=8,

∵四边形PMQR、四边形ARQN是矩形,

∴S△PQM＝S△PRQ，S△ANQ＝S△ARQ,

∴S△APQ＝S△PRQ+ S△ARQ＝ S矩形PMNA=4;

(2)当PQx轴时，则PQ＝ ，,AP=2m,

∵PQ=AP

∴2m=,

∴m=

∴,

当PQ＝AQ时，则；

（3）∵△OAB是以AB为底的等腰三角形，

∴OA＝OB，

∵A（m, ）,B(n, )，

∴

∴mn=4.