题目内容
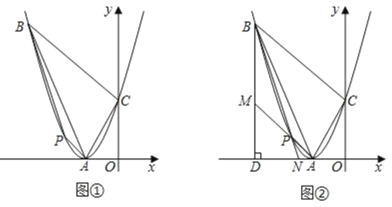
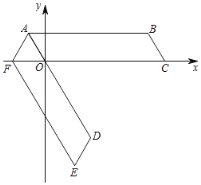
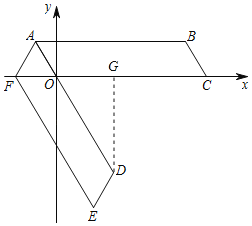
【题目】如图,四边形ABCO是平行四边形,OA=2,AB=8,点C在x轴的正半轴上,将平行四边形ABCO绕点A顺时针旋转得到平行四边形ADEF,AD恰好经过点O,点F恰好落在x轴的负半轴上.则点D的坐标是_____.
【答案】(3,﹣3![]() )
)
【解析】
根据平行四边形的性质和旋转的性质得出∠DOC=60°,可以求得点D的坐标.
解:作DG⊥OC于G,如图:
由旋转可得:OA=AF=2,∠BAO=∠FAO,
∴∠AFO=∠AOF,
∵AB∥OF,
∴∠BAO=∠OAF,
∴∠BAO=∠AOF=∠AFO=∠FAO,
∴△AFO是等边三角形,
∴∠DOC=∠AOF=60°,
∵AO=2,AD=AB=8,
∴OD=6,
∴OG=![]() OD=3,DG=
OD=3,DG=![]() ,
,
∴点D的坐标为(3,﹣3![]() );
);
故答案为:(3,﹣3![]() ).
).

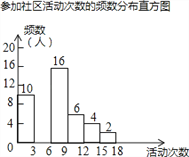
【题目】射阳县实验初中为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表
活动次数x | 频数 | 频率 |
0<x≤3 | 10 | 0.20 |
3<x≤6 | a | 0.24 |
6<x≤9 | 16 | 0.32 |
9<x≤12 | 6 | 0.12 |
12<x≤15 | m | b |
15<x≤18 | 2 | n |
根据以上图表信息,解答下列问题:
(1)表中a= ,b= ;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
【题目】某中学形展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示.

(1)根据图示填写下表:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | ||
九(2) | 85 | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.