题目内容
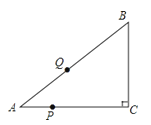
【题目】如图，AB与CD相交于点O，且∠OAD=∠OCB，延长AD、CB交于点P，那么图中的相似三角形的对数为 
【答案】2
【解析】解：如图，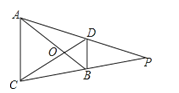
∵在△ABP与△CDP中，∠BAP=∠DCP，∠APB=∠CPD，
∴△ABP∽△CDP，
∴∠ABP=∠CDP，
∴∠ADO=∠CBO，
又∵∠OAD=∠OCB，
∴△OAD∽△OCB，
综上所述，图中的相似三角形有2对：△ABP∽△CDP，△OAD∽△OCB．
故答案是：2．
【考点精析】通过灵活运用相似三角形的判定，掌握相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）即可以解答此题．
练习册系列答案
相关题目
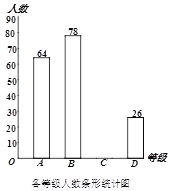
【题目】某电子品牌商下设台式电脑部、平板电脑部、手机部等．2018年的前五个月该品牌全部商品销售额共计600万元．下表表示该品牌商2018年前五个月的月销售额（统计信息不全）．图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图．
品牌月销售额统计表（单位：万元）
月份 | 1月 | 2月 | 3月 | 4月 | 5月 |
品牌月销售额 | 180 | 90 | 115 | 95 |
（
）该品牌5月份的销售额是 万元；
（
）手机部5月份的销售额是 万元；
小明同学观察图1后认为，手机部5月份的销售额比手机部4月份的销售额减少了，你同意他的看法吗？请说明理由；
（
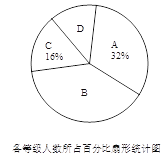
）该品牌手机部有A、B、C、D、E五个机型，图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图．则5月份 机型的销售额最高，销售额最高的机型占5月份该品牌销售额的百分比是 ．
