题目内容
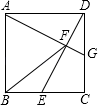
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
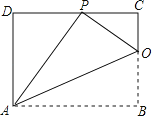
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
【答案】(1)证明见解析;(2)4.
【解析】
(1)由矩形的性质可知∠B=∠C=∠D=90°,由翻折可知,∠APC=90°,利用余角的性质可知∴∠DAP=∠CPO,即可由相似三角形的判定推出结论;
(2)利用正弦函数的定义及相似三角形的性质可直接求出CP的长.
(1)证明:∵四边形ABCD为矩形,
∴∠B=∠C=∠D=90°,
由折叠,可知:∠APO=∠B=90°,
∴∠APD+∠CPO=90°,
∵∠APD+∠DAP=90°,
∴∠DAP=∠CPO,
∴△PDA∽△OCP;
(2)由折叠,可知:∠APO=∠B=90°,AP=AB,PO=BO,
∴tan∠PAO=![]() ,
,
∵△PDA∽△OCP,
∴![]() ,
,
∵AD=8,
∴CP=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目