Question

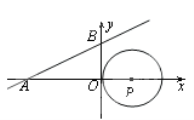
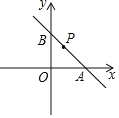
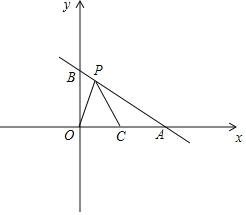
【题目】如图，在平面直角坐标系中，已知，A(2,0)，B（0，2），C(,0)，点P（m，n）为直线AB上一动点，若∠OPC＝30°，则m的值为_____．

Answer 1

【答案】或．

【解析】

首先证明△OPC∽△OAP，列出比例式求出OP＝，然后求得直线AB的函数解析式，根据函数图象上点的坐标特点用m表示出n，从而根据OP＝＝求得m的值．

解：∵，

∴OA＝2，OB＝2，OC＝，

∴tan∠BAO＝，

∴∠BAO＝30°，

∵∠OPC＝30°，

∴∠OPC＝∠OAP，

∵∠POC＝∠AOP，

∴△OPC∽△OAP，

∴，即，

解得，OP＝（负值已舍去），

设过点，B（0，2）的直线解析式为y＝kx+b，

则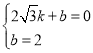，解得，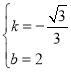

即直线AB的函数解析式为y＝﹣x+2，

∵P（m，n）为直线AB上一动点，

∴n＝﹣m+2，

∵OP＝，

∴，

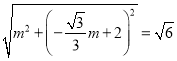解得，m1＝，m2＝，

故答案为：或．