题目内容
【题目】如图,点C,D在线段AB上,CD2=ACDB,且△PCD是等边三角形.
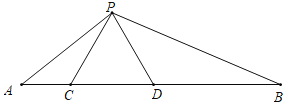
(1)证明:△ACP∽△PDB;
(2)求∠APB的度数.
【答案】(1)见解析;(2)∠APB=120°.
【解析】
(1)通过△PCD是等边三角形,得出∠ACP=∠PDB,再通过CD2=ACDB得出![]() ,从而证明△ACP∽△PDB;
,从而证明△ACP∽△PDB;
(2)由△ACP∽△PDB可得∠APC=∠PBD,进而得出∠APC+∠BPD=60,从而∠APB的度数可求.
(1)∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,
∴∠ACP=∠PDB=120°,
∵CD2=ACDB,由PC=PD=CD可得:PCPD=ACDB,
即![]() ,
,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD.
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°.
∴∠APB=∠CPD+∠APC+∠BPD=120°.

练习册系列答案
相关题目
【题目】如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届 | 2012届 | 2013届 | 2014届 | 2015届 | |
参与实验的人数 | 106 | 110 | 98 | 104 | 112 |
右手大拇指在上的人数 | 54 | 57 | 49 | 51 | 56 |
频率 | 0.509 | 0.518 | 0.500 | 0.490 | 0.500 |
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )

A. 0.6 B. 0.5 C. 0.45 D. 0.4