Question

【题目】小明准备给长米，宽米的长方形空地栽种花卉和草坪，图中I、II、III三个区域分别栽种甲、乙、丙三种花卉，其余区域栽种草坪．四边形和均为正方形，且各有两边与长方形边重合；矩形（区域II）是这两个正方形的重叠部分，如图所示．

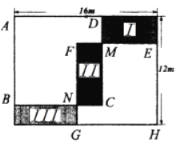
（1）若花卉均价为元，种植花卉的面积为，草坪均价为元，且花卉和草坪栽种总价不超过元，求的最大值．

（2）若矩形满足．

①求，的长．

②若甲、乙、丙三种花卉单价分别为元，元，元，且边的长不小于边长的倍．求图中I、II、III三个区域栽种花卉总价的最大值．

Answer 1

【答案】（1）的最大值为52米2；（2）①MF的长为4米，FN的长为8米；②的最大值为元．

【解析】

（1）先求出长方形空地的面积，从而可得栽种草坪的面积，再根据“总价不超过元”建立一元一次不等式，然后求解即可得；

（2）①设，，根据正方形的性质、线段的和差可得MF、FN的长，再根据可得a、b的关系等式，由此即可得出答案；

②先在①的基础上，求出W关于a的函数表达式，再根据题意求出a的取值范围，然后利用二次函数的性质求解即可得．

（1）长方形空地的面积为（米2）

由题意得：

解得

故的最大值为52米2；

（2）①设，

四边形和均为正方形

，

，

又

解得

（米），（米）

答：MF的长为4米，FN的长为8米；

②由①可知，，即

则由题意得：

又且

且

解得

由二次函数的性质可知，当时，随a的增大而减小

则当时，取得最大值，最大值为（元）

答：图中I、II、III三个区域栽种花卉总价的最大值为7040元．