Question

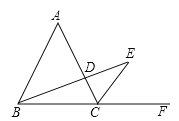
【题目】如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，对角线BD平分∠ABC，过点D作DE⊥BC，垂足为E，若BD＝，BC=6，则AB=（　　）

A.B.2C.D.3

Answer 1

【答案】B

【解析】

过点D作DH⊥AB，交BA的延长线于H，可证四边形BEDH是正方形，可得BD=BE，DE=HD，∠HDE=∠ADC=90°，由“ASA”可证△ADH≌△CDE，可得AH=CE=2，即可求解．

解：如图，过点D作DH⊥AB，交BA的延长线于H，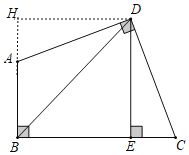

∵∠ABC=∠ADC=90°，DH⊥AB，DE⊥BC，
∴四边形BEDH是矩形，
∵BD平分∠ABC，
∴∠DBE=45°，
∴∠DBE=∠BDE=45°，
∴BE=DE，
∴四边形BEDH是正方形，
∴BD=BE，DE=HD，∠HDE=∠ADC=90°，
∴HD=DE=HB=BE=4，∠HDA=∠CDE，
又∵∠H=∠DEC=90°，
∴△ADH≌△CDE（ASA），
∴CE=AH=BC-BE=6-4=2，
∴AB=BH-AH=4-2=2，
故选：B．