题目内容
如图，已知AB⊥AD，CD⊥AD，垂足分别为A、D，AD=6，AB=5，CD=3，P是线段AD上的一个动点，设AP=x，DP=y，a=| x2+25 |
| y2+9 |
分析：首先确定当BPC三点在同一直线时，a的值最小．然后根据相似三角形的性质计算．
解答：解：由题意可得，当BPC三点在同一直线时，a的值最小．
则△ABP∽△DCP，
x=
，y=
，
则a的最小值是10．
则△ABP∽△DCP，
x=
| 15 |
| 4 |
| 9 |
| 4 |
则a的最小值是10．
点评：此题考查了线路最短的问题，确定动点为何位置是关键综合运用相似三角形的知识．
练习册系列答案
优生乐园系列答案
新编小学单元自测题系列答案
相关题目
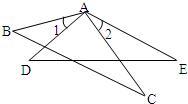16、如图，已知AB=AD，∠1=∠2，要使△ABC≌△ADE，还需添加的条件是（只需填一个）
25、如图，已知AB=AD，AC=AE，∠1=∠2，求证△ABC≌△ADE．
27、如图，已知AB=AD，BC=DC，BD交AC于点O，请分别说明下列判断成立的理由：
如图，已知AB=AD，点E、F分别是CD、BC的中点，BF=CE，求证：AE=AF．