题目内容
已知点P是边长为4的正方形ABCD内一点,且PB="3" , BF⊥BP,垂足是点B, 若在射线BF上找一点M,使以点B, M, C为顶点的三角形与△ABP相似,则BM为___________.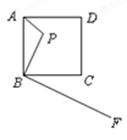
3或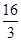 .
.
解析试题分析:∵∠ABC=∠FBP=90°
∴∠ABP=∠CBF
当△ABP∽△MBC时,BM:AB=BC:BP,得BM=4×4÷3=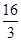 ;
;
当△ABP∽△CBM时,BM:BP=CB:AB,得BM=4×3÷4=3.
故答案是3或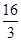 .
.
考点:1.相似三角形的性质2.正方形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设 是三个互不相同的正数,如果
是三个互不相同的正数,如果 ,那么( )
,那么( )
A. | B. | C. | D.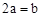 |
如图,ABCD是边长为1的正方形,对角线AC所在的直线上有两点M、N,使∠MBN=1350,则MN的最小值是不是( )
A.1+ | B.2+ | C.3+ | D.2 |

 ,则△EFD与△ABC的面积比为 .
,则△EFD与△ABC的面积比为 .


 OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
OA;(4)AD2+BE2=2OP•OC.其中正确的结论有【 】
 (
( 均不为0),则
均不为0),则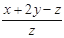 的值为 .
的值为 .