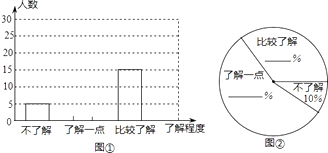
题目内容
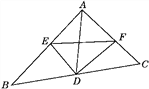
【题目】如图,△ABC中,AD是BC边上的中线,以D为顶点作∠EDF=90°,DE,DF分别交AB,AC于E,F,且BE2+CF2=EF2,求证:△ABC为直角三角形.
【答案】见解析
【解析】试题分析:延长FD到点M,使DM=DF,连接BM,可证得△CDF≌△BDM,根据全等三角形的性质可得∠DBM=∠C,BM=CF,由∠EDF=90°,MD=FD,根据线段垂直平分线的性质可得EM=EF;再由BE2+CF2=EF2,可得BE2+BM2=EM2,根据勾股定理的逆定理可得△BEM为直角三角形,再证得BM∥AC,由平行线的性质即可证得∠BAC=90°,结论得证.
试题解析:
证明:延长FD至M,使MD=FD,连接MB,ME,如图所示,
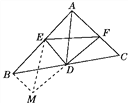
∵D为BC的中点,∴BD=DC,又MD=FD,∠BDM=∠CDF,
∴△BDM≌△CDF(SAS),∴∠DBM=∠C,BM=CF,
∵∠EDF=90°,MD=FD,∴EM=EF,
∵BE2+CF2=EF2,∴BE2+BM2=EM2,
即△BEM为直角三角形,且∠EBM=90°.
由∠DBM=∠C知,BM∥AC,∴∠BAC=180°-∠EBM=90°,
即△ABC为直角三角形.

练习册系列答案
相关题目