题目内容
如图,己知双曲线y=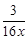 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(1)求△OPQ的面积.
(2)试说明:△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点,CA=a(0<a<1),CD⊥AB于D,DE⊥OB于E.
①a为何值时,CE=AC?
②线段OA上是否存在点C,使CE∥AB?若存在这样的点,请求出点C的坐标:若不存在,请说明理由.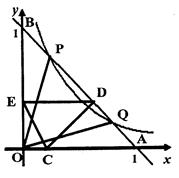
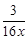 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.(1)求△OPQ的面积.
(2)试说明:△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点,CA=a(0<a<1),CD⊥AB于D,DE⊥OB于E.
①a为何值时,CE=AC?
②线段OA上是否存在点C,使CE∥AB?若存在这样的点,请求出点C的坐标:若不存在,请说明理由.

解:(1)∵A(1,0)B(0,1)
∴OB=OA,∠OBA=∠OAB,直线AB的解析式为y=-x+1
∵双曲线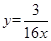 (x>0)与经过点A,B的直线交于P、Q两点
(x>0)与经过点A,B的直线交于P、Q两点
∴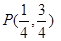
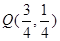
∵
∴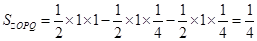
(2) 由(1)得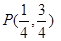
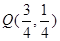
∵A(1,0)B(0,1)
∴PB=AQ
∵OB=OA,∠OBA=∠OAB
∴△OAQ≌△OBP
(3)①解:作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,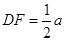
∴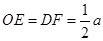
在直角三角形EOC中,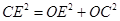
若CE=AC,则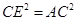
∴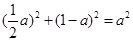
解之得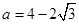 或
或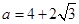
∵0<a<1
∴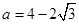
②若CE∥AB,则有∠ECO=∠OEC=∠B=∠A=45°
∴OE=OC=1-a
作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,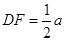
∴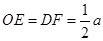
∴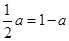
解之得
∴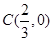
∴OB=OA,∠OBA=∠OAB,直线AB的解析式为y=-x+1
∵双曲线
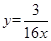 (x>0)与经过点A,B的直线交于P、Q两点
(x>0)与经过点A,B的直线交于P、Q两点∴
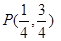
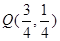
∵

∴
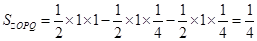
(2) 由(1)得
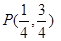
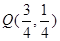
∵A(1,0)B(0,1)
∴PB=AQ
∵OB=OA,∠OBA=∠OAB
∴△OAQ≌△OBP
(3)①解:作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,
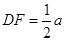
∴
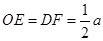
在直角三角形EOC中,
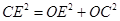
若CE=AC,则
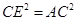
∴
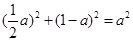
解之得
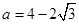 或
或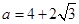
∵0<a<1
∴
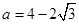
②若CE∥AB,则有∠ECO=∠OEC=∠B=∠A=45°
∴OE=OC=1-a
作DF⊥AO
易得OEFD为矩形
等腰直角三角形ACD中,
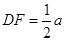
∴
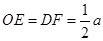
∴
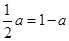
解之得

∴
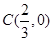
(1)直接求三角形的面积较繁,此题用补的方法求较容易,把△OPQ补成△AOB
减去△BOP和△AOQ的面积即可
(2)利用点的坐标,求出线段长,找出三角形全等的条件
(3)作辅助线,结合勾股定理,用a的代数式表示CE,根据CE=AC,列出a的方程即可;根据CE∥AB,等腰三角形的三线合一,直角三角形斜边的中线等于斜边的一半,列出a的方程即可
减去△BOP和△AOQ的面积即可
(2)利用点的坐标,求出线段长,找出三角形全等的条件
(3)作辅助线,结合勾股定理,用a的代数式表示CE,根据CE=AC,列出a的方程即可;根据CE∥AB,等腰三角形的三线合一,直角三角形斜边的中线等于斜边的一半,列出a的方程即可

练习册系列答案
相关题目
 上关于原点对称的任意两点,AC∥y轴,BD∥y轴,则四边形ACBD的面积S满足( )
上关于原点对称的任意两点,AC∥y轴,BD∥y轴,则四边形ACBD的面积S满足( )
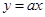 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点

 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值? 是反比例函数图象上的一动点,其中
是反比例函数图象上的一动点,其中 过点
过点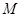 作直线
作直线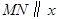 轴,交
轴,交 轴于点
轴于点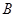 ;过点
;过点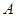 作直线
作直线 轴交
轴交 ,交直线
,交直线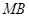 于点
于点 .当四边形
.当四边形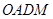 的面积为6时,请判断线段
的面积为6时,请判断线段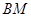 与
与 的大小关系,并说明理由.
的大小关系,并说明理由. 的上的两个点,若x2>x1>0,则( )
的上的两个点,若x2>x1>0,则( ) 的图象上有两点(-1,y1),
的图象上有两点(-1,y1), ,则y1-y2的值是【 】
,则y1-y2的值是【 】 与正比例函数
与正比例函数 在同一坐标系内的大致图像为( ).
在同一坐标系内的大致图像为( ).
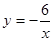 图像上的是 ( )
图像上的是 ( ) .(-2,-4);
.(-2,-4);  .(2,3);
.(2,3);  .(-6,1);
.(-6,1);  .(-
.(- ,3).
,3).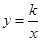 的图象经过点A(-1, 2),则当x>1时,函数值y的取值范围是( )
的图象经过点A(-1, 2),则当x>1时,函数值y的取值范围是( )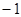
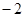
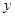 cm与宽
cm与宽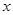 cm之间的函数关系用图象表示大致是
cm之间的函数关系用图象表示大致是 