题目内容
 一个一元一次不等式组的解集如图所示,则这个一元一次不等式组可以是( )
一个一元一次不等式组的解集如图所示,则这个一元一次不等式组可以是( )分析:根据数轴写出x的取值范围,再分别解出四个不等式组的解集,即可选出答案.
解答:解:根据数轴可得x的取值范围是1<x≤2,
A、
,
整理x+1>3x-1得,
2x<2,
解得:x<1,
整理
x≤2-
x得,
x≤2,
故不等式组的解集为:x<1,故此选项错误;
B、
,
整理-5x≤4x-9得,
9x≥9,
解得:x≥1,
整理2(1-x)>x-4得,
-3x>-6,
解得:x<2,
故解不等式组可得解集为1≤x<2,故此选项错误;
C、
,
整理
x+
>
x+
得,
x>
,
解得:x>1,
整理-3x≥x-8得,
-4x≥-8,
解得:x≤2,
故解不等式组可得解集为1<x≤2,故此选项正确;
D、
,
整理3x≤4-2(1+x)得,
5x≤2,
解得:x≤
,
整理-x<-1得,
x>1,
解得:x>1,
故解不等式组可得无解,故此选项错误;
故选:C.
A、
|
整理x+1>3x-1得,
2x<2,
解得:x<1,
整理
| 2 |
| 3 |
| 1 |
| 3 |
x≤2,
故不等式组的解集为:x<1,故此选项错误;
B、
|
整理-5x≤4x-9得,
9x≥9,
解得:x≥1,
整理2(1-x)>x-4得,
-3x>-6,
解得:x<2,
故解不等式组可得解集为1≤x<2,故此选项错误;
C、
|
整理
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 6 |
解得:x>1,
整理-3x≥x-8得,
-4x≥-8,
解得:x≤2,
故解不等式组可得解集为1<x≤2,故此选项正确;
D、
|
整理3x≤4-2(1+x)得,
5x≤2,
解得:x≤
| 2 |
| 5 |
整理-x<-1得,
x>1,
解得:x>1,
故解不等式组可得无解,故此选项错误;
故选:C.
点评:此题主要考查了解不等式组,以及在数轴上表示解集,关键是正确解出不等式的解集.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
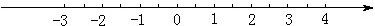
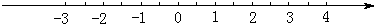
 一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为
一个一元一次不等式组的解集在数轴上表示如图所示,则该不等式组的解集为