题目内容
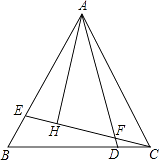
【题目】如图,△ABC是等边三角形,点D、E分别是BC边、AB边上的点,且BE=CD,连接AD、CE交于点F,过A作AH⊥CE于H,
(1)求证:∠BCE=∠CAD;
(2)直接写出∠CFD的度数;并写出线段AF与线段HF的数量关系.(无需解答过程)
【答案】
(1)
证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠ACD=60°,
在△BCE与△ACD中, 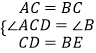 ,
,
∴△BCE≌△ACD,
∴∠BCE=∠CAD
(2)
∠CFD=60°,AF=2HF,
∵∠BCE=∠CAD,∠ACF+∠CAF=60°,
∴∠DAC+∠ACF=60°,
∵∠CFD=∠DAC+∠ACF,
∴∠CFD=60°,
∵AH⊥CE,
∴∠HAF=30°,
∴AF=2HF.
【解析】(1)由△ABC是等边三角形,于是得到AB=AC=BC,∠B=∠ACD=60°,证得△BCE≌△ACD,根据全等三角形的性质即可得到结论;(2)由(1)证得∠BCE=∠CAD,于是推出∠DAC+∠ACF=60°,根据外角的性质得到∠CFD=∠DAC+∠ACF,于是得到∠CFD=60°,根据直角三角形的性质即可得到结论.
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
相关题目