Question

【题目】如图，在△ABC中，∠C=90°，∠B=30°，以A为圆心，任意长为半径画弧分别交AB、AC于点M和N ， 再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于点P ， 连结AP并延长交BC于点D ， 则下列说法中正确的个数是（　　）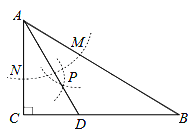
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC ．
A.1
B.2
C.3
D.4

Answer 1

【答案】D
【解析】①AD是∠BAC的平分线，说法正确； ②∵∠C=90°，∠B=30°，
∴∠CAB=60°，
∵AD平分∠CAB ，
∴∠DAB=30°，
∴∠ADC=30°+30°=60°，
因此∠ADC=60°正确；
③∵∠DAB=30°，∠B=30°，
∴AD=BD ，
∴点D在AB的中垂线上，故③说法正确，
④∵∠C=90°，∠B=30°，
∴AB=2AC ，
选：D ．