题目内容
【题目】已知OP平分∠AOB,点Q在OP上,点M在OA上,且点Q,M均不与点O重合.在OB上确定点N,使QN =QM,则满足条件的点N的个数为( )
A.1 个B.2个C.1或2个D.无数个
【答案】C
【解析】
分两种情况:QM⊥OA和QM不垂直OA,当QM⊥OA时,N有一点;当QM不垂直OA时,N有两点.故可得解.
当QM⊥OA时,N有一点,如图所示,
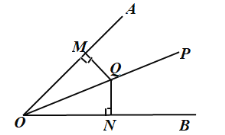
过点Q作QN⊥OB,垂足为N,
∵OP平分∠AOB,QM⊥OA,
∴QM=QN;
当QM不垂直OA时,N有两点,如图所示,
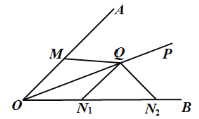
在OA,OB上分别截取OM=ON1,连接QM,QN1,
∵OP平分∠AOB,
∴∠MOQ=∠N1OQ
在△MOQ和△N1OQ中,
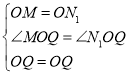
∴△MOQ≌△N1OQ
∴QM=QN1;
作∠QN1N2=∠QN2N1,则有QN1=QN2,
∴QM=QN2.
所以,满足条件的点N的个数为1个或2个.
故选:C.

练习册系列答案
相关题目