Question

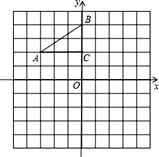
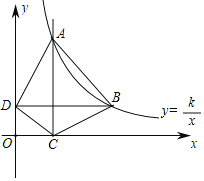
【题目】如图，在平面直角坐标系中，函数的图象经过点和点.过点作轴，垂足为点，过点作轴，垂足为点，连结、、、.点的横坐标为.

（1）求的值.

（2）若的面积为.

①求点的坐标.

②在平面内存在点，使得以点、、、为顶点的四边形是平行四边形，直接写出

符合条件的所有点的坐标.

Answer 1

【答案】（1）4；（2）①点的坐标为．②、、

【解析】

（1）利用待定系数法将A点代入，即可求函数解析式的k值；

（2）用三角形ABD的面积为4,列方程，即可求出a的值,可得点的坐标；

（3）E的位置分三种情况分析，由平行四边形对边平行的关系，用平移规律求对应点的坐标.

（1）函数的图象经过点，

（2）①如图，设AC与BD交与M,

点的横坐标为，点在的图象上，

点的坐标为．

∵轴，轴，

，．

∵的面积为，

．

．

．

点的坐标为．

②∵C(1,0)

∴AC=4

当以ACZ作为平行四边形的边时，BE=AC=4

∴

∴

∴、

当AC作为平行四边形的对角线时，AC中点为

∴BE中点为（1，2）设E(x，y)

∵点的坐标为

则

解得：

∴

综上所述：在平面内存在点，使得以点、、、为顶点的四边形是平行四边形，符合条件的所有点的坐标为：、、

故答案为：、、