题目内容
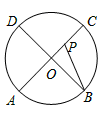
如图，两个同心圆的半径分别为4cm和5cm，大圆的一条弦AB与小圆相切，则弦AB的长为（ ）
| A．3cm | B．4cm | C．6cm | D．8cm |
C.
试题分析：首先连接OC，AO，由切线的性质，可得OC⊥AB，由垂径定理可得AB=2AC，然后由勾股定理求得AC的长，继而可求得AB的长．
如图，连接OC，AO，
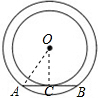
∵大圆的一条弦AB与小圆相切，
∴OC⊥AB，
∴AC=BC=
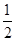AB，∵OA=5cm，OC=4cm，
在Rt△AOC中，AC=
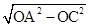=3cm，∴AB=2AC=6（cm）．
故选C．
考点: 1.切线的性质；2.勾股定理；3.垂径定理．
练习册系列答案
阳光课堂课时作业系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
的中点，点P是直径MN上一动点，若⊙O的半径为1，则AP＋BP的最小值是 ．
A．
B．
C．
D．