题目内容
【题目】已知抛物线![]() 和直线y=(k+1)x+(k+1)2.
和直线y=(k+1)x+(k+1)2.
(1)求证:无论k取何值,抛物线总与x轴有两个不同的交点;
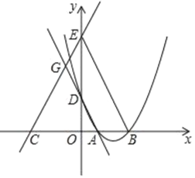
(2)如果抛物线与x轴的交点A,B在原点的右边,直线与x轴的交点C在原点的左边,又抛物线、直线分别交y轴于点D,E,直线AD交直线CE于点G(如图),且CAGE=CGAB,求抛物线的解析式.
【答案】(1)见解析;(2)y=x2﹣4x+3.
【解析】
(1)求出根的判别式并化为完全平方形式,利用一元二次方程的根的判别式大于0确定出抛物线与x轴的交点坐标有两个;
(2)由CAGE=CGAB得出△CAG∽△CBE,进而判断出△OAD∽△OBE得出OA:OB=OD:OE,抛物线与x轴交点是AB两点,根据根与系数的关系可得OAOB=![]() .根据图象与y轴交点可得:OD=
.根据图象与y轴交点可得:OD=![]() ,OE=(k+1)2,从而求得OB=k+1,进而代入抛物线解析式求出k值即可.
,OE=(k+1)2,从而求得OB=k+1,进而代入抛物线解析式求出k值即可.
解:(1)证明:∵△=(k+2)2﹣4×1×![]() =k2﹣k+2=
=k2﹣k+2=![]() ,
,
∵![]() ,
,
∴△>0,
故无论k取何实数值,抛物线总与x轴有两个不同的交点;
(2)∵CAGE=CGAB,
∴CA:CB=CG:CE,
∵∠ACG=∠BCE,
∴△CAG∽△CBE,
∴∠CAG=∠CBE,
∵∠AOD=∠BOE,
∴△OAD∽△OBE,
∴OA:OB=OD:OE,
∵抛物线与x轴的交点A、B在原点的右边,
直线与x轴的交点C在原点的左边,
又抛物线、直线分别交y轴于点D、E,
∴OAOB=![]() ,OD=
,OD=![]() ,OE=(k+1)2,
,OE=(k+1)2,
∴OAOB=OD,由OA:OB=OD:OE
∴OA:OB=(OAOB):OE,
∴OB2=OE,
∴OB=k+1,
∴点B(k+1,0),
将点B代入抛物线y=x2﹣(k+2)x+![]() 得:
得:
(k+1)2﹣(k+2)(k+1)﹣![]() =0,
=0,
解得:k=2,
∴抛物线的解析式为:y=x2﹣4x+3.





