Question

【题目】如图，反比例函数y=与一次函数y=k2x+b图象的交点为A（m，1），B（﹣2，n），OA与x轴正方向的夹角为α，且tanα=．

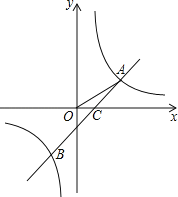
（1）求反比例函数及一次函数的表达式；

（2）设直线AB与x轴交于点C，且AC与x轴正方向的夹角为β，求tanβ的值．

Answer 1

【答案】（1）y=，y=x﹣1．（2）．

【解析】

试题分析：（1）过点A作AE⊥x轴于点E，根据tanα=可得出m的值，进而得出反比例函数的解析式，根据B（﹣2，n）在反比例函数y=的图象上得出B点坐标，再把A、B两点的坐标代入直线y=k2x+b即可得出其解析式；

（2）先求出C点坐标，再由A点坐标可得出AE的长，根据锐角三角函数的定义即可得出结论．

解：（1）过点A作AE⊥x轴于点E，

∵tan∠AOE=tanα=，

∴OE=4AE．

∵A（m，1），

∴AE=1，

∴OE=4，

∴A（4，1）．

∵点A在反比例函数y=的图象上，

∴k1=4，

∴反比例函数的解析式为y=．

∵B（﹣2，n）在反比例函数y=的图象上，

∴n=2，

∴B（﹣2，﹣2）．

将A、B两点的坐标代入直线y=k2x+b得，

，解得，

∴直线AB的解析式为y=x﹣1．

（2）∵直线AB的解析式为y=x﹣1，令y=0，则x=2，

∴C（2，0）．

∵A（4，1），

∴CE=2，AE=1，

∴tanβ==．