题目内容
【题目】如图,矩形ABCD中,AB=10,BC=5,点P为AB边上一动点(不与点A,B重合),DP交AC于点Q.
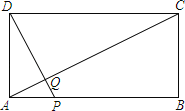
(1)求证:△APQ∽△CDQ;
(2)当PD⊥AC时,求线段PA的长度;
(3)当点P在线段AC的垂直平分线上时,求sin∠CPB的值.
【答案】(1)见解析;(2)AP=![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)根据矩形的性质和相似三角形的判定定理证明即可;
(2)根据垂直的定义、相似三角形的性质列出比例式,计算即可;
(3)连接PC,根据线段垂直平分线的性质得到PC=PA,设PA=x,根据勾股定理列出关于x的方程,解方程即可.
(1)证明:∵四边形ABCD是矩形,
∴DC∥AB,
∴∠QAP=∠QCD,∠QPA=∠QDC,
∴△APQ∽△CDQ;
(2)解:∵PD⊥AC,
∴∠QDC+∠QCD=90°,又∠QDC+∠QDA=90°,
∴∠QCD=∠QDA,又∠DAP=∠CDA=90°,
∴△DAP∽△CDA,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,AP=![]() ;
;
(3)解:连接PC,
∵点P在线段AC的垂直平分线上,
∴PC=PA,
设PA=x,则PC=x,PB=10﹣x,
由勾股定理得,PC2=PB2+BC2,即x2=(10﹣x)2+25,
解得,x=![]() ,
,
∴PC=PA=![]() ,
,
∴sin∠CPB=![]() =
=![]() .
.

练习册系列答案
相关题目