题目内容
【题目】在等腰△ABC中，AB=AC，一边上的中线BD 将这个三角形的周长分为15和12两个部分，则该等腰三角形的底边长为 （ ）
A．7 B．10 C．7或10 D．7或11
【答案】D
【解析】
试题分析：根据题意画出图形，设等腰三角形的腰长为a，底边为b，根据重点定义得到AD与DC相等都等于腰长a的一半，AC边上的中线BD将这个三角形的周长分为AB+AD和BC+CD两部分，分别表示出两部分，然后分AB+AD=15，BC+CD=12或AB+AD=12，BC+CD=15两种情况分别列出方程组，分别求出方程组的解即可得到a与b的两对值，根据三角形的两边之和大于第三边判定能否构成三角形，即可得到满足题意的等腰三角形的底边长．
依题意可得：这一边上的中线为腰上的中线，画出图形如下：
设这个等腰三角形的腰长为a，底边长为b，
∵D为AC的中点，∴AD=DC=
，
根据题意的：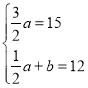
或
，
解得
或
又∵三边长10、10、7和8、8、11均可以构成三角形，
∴底边长为7或11．
故答案为：D
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
