题目内容
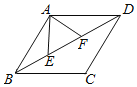
【题目】如图,菱形ABCD的边长为2![]() ,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
,∠ABC=60°,点E、F在对角线BD上运动,且EF=2,连接AE、AF,则△AEF周长的最小值是( )
A.4B.4+![]() C.2+2
C.2+2![]() D.6
D.6
【答案】D
【解析】
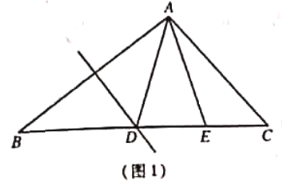
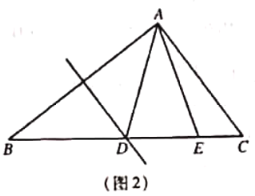
作AH∥BD,使得AH=EF=2,连接CH交BD于F,则AE+AF的值最小,进而得出△AEF周长的最小值即可.
解:如图作AH∥BD,使得AH=EF=2,连接CH交BD于F,则AE+AF的值最小,即△AEF的周长最小.
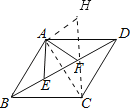
∵AH=EF,AH∥EF,
∴四边形EFHA是平行四边形,
∴EA=FH,
∵FA=FC,
∴AE+AF=FH+CF=CH,
∵菱形ABCD的边长为2![]() ,∠ABC=60°,
,∠ABC=60°,
∴AC=AB=2![]() ,
,
∵四边形ABCD是菱形,
∴AC⊥BD,
∵AH∥DB,
∴AC⊥AH,
∴∠CAH=90°,
在Rt△CAH中,CH=![]()
∴AE+AF的最小值4,
∴△AEF的周长的最小值=4+2=6,
故选:D.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目