题目内容
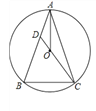
【题目】已知四边形ABCD是菱形,AC、BD交于点E,点F在CB的延长线上,连结EF交AB于H,以EF为直径作⊙O,交直线AD于A、G两点,交BC于K点.
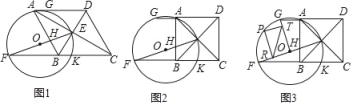
(1)如图1,连结AF,求证:四边形AFBD是平行四边形;
(2)如图2,当∠ABC=90°时,求tan∠EFC的值;
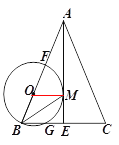
(3)如图3,在(2)的条件下,连结OG,点P在弧FG上,过点P作PT∥OF交OG于T,PR∥OG交OF于R点,连结TR,若AG=2,在点P运动过程中,探究线段TR的长是否为定值,如果是,则求出这个定值;如果不是,请说明理由.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接AF,由EF是⊙O的直径知FA⊥AC,由四边形ABCD是菱形知BD⊥AC、AD∥FB,据此可得FA∥BD,即可得证;
(2)连接EK,先证四边形ABCD是正方形,由EF是⊙O的直径知FK⊥EK,设BK=EK=a,则BC=AD=FB=2a,根据tan∠EFC=![]() 可得答案;
可得答案;
(3)连接OP、FA,过点O作OM⊥GD,并延长MO交FC于点N,先证四边形PROT是矩形得RT=OP=OG,由MN⊥FC知tan∠EFC=tan∠GOM=![]() ,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=
,由AG=2、OM⊥GD知GM=1、OM=3,由勾股定理可得GO=![]() ,继而可得答案.
,继而可得答案.
(1)如图1,连接AF,

∵EF是⊙O的直径,
∴∠FAC=90°,即FA⊥AC,
∵四边形ABCD是菱形,
∴BD⊥AC,AD∥BC、即AD∥FB,
∴FA∥BD,
∴四边形AFBD是平行四边形;
(2)如图2,连接EK,
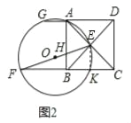
∵∠ABC=90°,四边形ABCD是菱形,
∴四边形ABCD是正方形,
∵EF是⊙O的直径,
∴FK⊥EK,
设BK=EK=a,则BC=AD=FB=2a,
则tan∠EFC=![]() =
=![]() ;
;
(3)TR的长是定值,
如图3,连接OP、FA,过点O作OM⊥GD,并延长MO交FC于点N,

∵EF是⊙O的直径,
∴FA⊥EA,
又∵四边形ABCD是正方形,
∴∠BAC=45°,
∴∠GAF=45°,
∴∠GOF=90°,
∵PT∥OF、PR∥OG,
∴四边形PROT是矩形,
∴RT=OP=OG,
∵OM⊥GD、GD∥FC,
∴MN⊥FC,
∴tan∠EFC=tan∠GOM=![]() ,
,
∵AG=2、OM⊥GD,
∴GM=1,
∴OM=3,
由勾股定理可得GO=![]() ,
,
∴RT=![]() .
.