题目内容
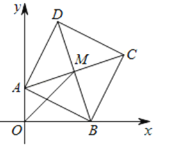
【题目】如图,在平面直角坐标系中,正方形ABCD顶点A的坐标为(0,4),B点在x轴上,对角线AC,BD交于点M,OM=6![]() ,则点C的坐标为_____.
,则点C的坐标为_____.
【答案】(12,8)
【解析】
过点C作CE⊥x轴于点E,过点M作MF⊥x轴于点F,连结EM,根据正方形的性质可以得出F是OE的中点,就可以得出MF是梯形AOEC的中位线,证明△AOB≌△BEC就可以得出OB=CE,AO=BE,就可以求得△OME是等腰直角三角形,由勾股定理就可以求出OE的值,从而得出C点的纵坐标.
过点C作CE⊥x轴于点E,过点M作MF⊥x轴于点F,连结EM,
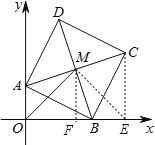
∴∠MFO=∠CEO=∠AOB=90,AO∥MF∥CE,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90![]() ,AM=CM,
,AM=CM,
∴∠OAB=∠EBC,OF=EF,
∴MF是梯形AOEC的中位线,
∴MF=![]() (AO+EC),
(AO+EC),
∵MF⊥OE,
∴MO=ME.
∵在△AOB和△BEC中,
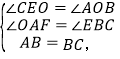
∴△AOB≌△BEC(AAS),
∴OB=CE,AO=BE.
∴MF=![]() (BE+OB),
(BE+OB),
又∵OF=FE,
∴△MOE是直角三角形,
∵MO=ME,
∴△MOE是等腰直角三角形,
∴![]()
∴A(0,4),
∴OA=4,
∴BE=4,
∴OB=CE=8
∴C(12,8).
故答案为:(12,8).

练习册系列答案
相关题目







