题目内容
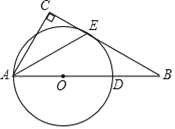
【题目】如图，
为
的中线，点
在
的延长线上的点，连接
，且
，过点
作
于点
，连接
，若
，则
的长为________________.
【答案】3
【解析】
过点A作AF⊥EF于点F，通过证明△AFD≌△BHD（AAS），Rt△CAF≌ Rt△EBH（HL），得到BH= HD+DF=2DH，又因为 
为
的中线，
，所以S△BHD=
S△BHA=×18=9=×HD·HB=×HD·2HD，从而求解.
解：如图：过点A作AF⊥EF于点F，
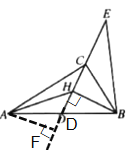
∵为的中线，，
∴AD=BD， ∠AFD=∠BHD=90°，
又∵∠ADF=∠BDH，
∴△AFD≌△BHD（AAS），
∴AF=BH，FD=HD，
∵在Rt△CAF和 Rt△EBH中，
∴Rt△CAF≌ Rt△EBH（HL）
∴EH=CF，
∴EH-CH=CF-CH，即EC=HF
∵BH=EC，EC=HF=HD+DF，HD=DF
∴BH= HD+DF=2DH,
∵为的中线，，
∴S△BHD=S△BHA=×18=9=×HD·HB=×HD·2HD,
解得：HD=3.
故答案为：3.
练习册系列答案
相关题目
