Question

【题目】如图，A、B、C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C地在A地北偏东75°方向．且BD=BC=30m．

（1）求∠ADC的度数；

（2）求A、D两地的距离.

Answer 1

【答案】（1）∠ADC的度数为75°；

（2）A、D两地的距离m.

【解析】试题分析：（1）过点D作DE//正北方向，则有∠ADE＝30°，∠CDE＝45°，这两个角相加即为∠ADC；（2）过点D作DH垂直于AC，垂足为H，求出∠DAC的度数，判断出△BCD是等边三角形，再利用三角函数求出AB的长，从而得到AB+BC+CD的长；

试题解析：

（1）过点D作DE//正北方向，如图所示：

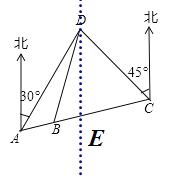
∴∠ADE＝30°，∠CDE＝45°，

∴∠ADC＝∠ADE+∠CDE＝75°；

（2）过点D作DH垂直于AC，垂足为H，如图所示：

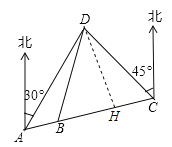
由题意可知∠DAC=75°-30°=45°，
∵△BCD是等边三角形，
∴∠DBC=60°，BD=BC=CD=30m，
∴DH= ，

∴AD= 。