题目内容
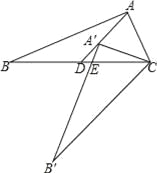
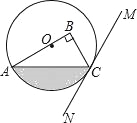
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
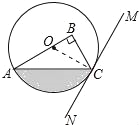
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
【答案】(1) MN是⊙O切线,理由详见解析;(2)![]() .
.
【解析】
试题分析:(1)MN是⊙O切线,只要证明∠OCM=90°即可.(2)求出∠AOC以及BC,根据S阴=S扇形OAC﹣S△OAC计算即可.
试题解析:(1)MN是⊙O切线.
理由:连接OC.
∵OA=OC,
∴∠OAC=∠OCA,
∵∠BOC=∠A+∠OCA=2∠A,∠BCM=2∠A,
∴∠BCM=∠BOC,
∵∠B=90°,
∴∠BOC+∠BCO=90°,
∴∠BCM+∠BCO=90°,
∴OC⊥MN,
∴MN是⊙O切线.
(2)由(1)可知∠BOC=∠BCM=60°,
∴∠AOC=120°,
在RT△BCO中,OC=OA=4,∠BCO=30°,
∴BO=![]() OC=2,BC=2
OC=2,BC=2![]()
∴S阴=S扇形OAC﹣S△OAC=![]() .
.

练习册系列答案
相关题目