题目内容
如图,已知直线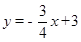 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.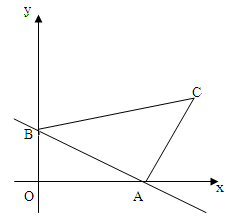
(1)求△AOB的面积;
(2)求点C坐标;
(3)点P是x轴上的一个动点,设P(x,0)
①请用x的代数式表示PB2、PC2;
②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;
如果存在,请求出点P的坐标.
(1)6;(2)(7,4);(3)① ,
, ;②存在这样的P点,P(3,0).
;②存在这样的P点,P(3,0).
解析试题分析:(1)先由直线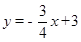 求出A、B两点的横坐标,即OA、OB的长,从而可求出△AOB的面积;
求出A、B两点的横坐标,即OA、OB的长,从而可求出△AOB的面积;
(2)过C点作CD⊥x轴,垂足为D,构造Rt△ADC.易证△OAB≌△DCA,从而可求出CD=4,OD=7,所以C点坐标为(7,4);
(3)①由(2)可知,PD=7-x,在Rt△OPB中, ,Rt△PCD中,
,Rt△PCD中,
②存在这样的P点.P(3,0).
试题解析:(1)由直线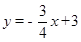 ,令y=0,得OA=x=4,令x=0,得OB=y=3,∴S△AOB=
,令y=0,得OA=x=4,令x=0,得OB=y=3,∴S△AOB= ×4×3=6;
×4×3=6;
(2)过C点作CD⊥x轴,垂足为D,
∵∠BAO+∠CAD=90°,∠ACD+∠CAD=90°,
∴∠BAO=∠ACD,
又∵AB=AC,∠AOB=∠CDA=90°,
∴△OAB≌△DCA,
∴CD=OA=4,AD=OB=3,则OD=4+3=7,
∴C(7,4);
(3)①由(2)可知,PD=7-x,
在Rt△OPB中,PB2=OP2+OB2=x2+9,
Rt△PCD中,PC2=PD2+CD2=(7-x)2+16=x2-14x+65,
②存在这样的P点.
设B点关于 x轴对称的点为B′,则B′(0,-3),
连接CB′,设直线B′C解析式为y=kx+b,将B′、C两点坐标代入,得 解得
解得
所以,直线B′C解析式为y=x-3,
令y=0,得P(3,0),此时|PC-PB|的值最大,
考点:一次函数综合题.

为保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为 cm,椅子的高度为
cm,椅子的高度为 cm,则
cm,则 应是
应是 的一次函数,下表列出两套符合条件的课桌椅的高度:
的一次函数,下表列出两套符合条件的课桌椅的高度:
| | 第一套 | 第二套 |
椅子高度 (cm) (cm) | 40 | 37 |
课桌高度 (cm) (cm) | 75 | 70 |
 与
与 的函数关系式.
的函数关系式.(2)现有一把高39 cm的椅子和一张高78.2 cm的课桌,它们是否配套?为什么?
某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
| | 甲 | 乙 |
| 进价(元/部) | 4000 | 2500 |
| 售价(元/部) | 4300 | 3000 |
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
 的解满足
的解满足 ,求关于
,求关于 的函数
的函数 的解析式.
的解析式.
 的图象经过点
的图象经过点 ,且与函数
,且与函数 的图象相交于点
的图象相交于点 .
. 的值;
的值; 轴的交点是B,函数
轴的交点是B,函数 轴的交点是C,求四边形
轴的交点是C,求四边形 的面积(其中O为坐标原点).
的面积(其中O为坐标原点).
