题目内容
(1)观察与发现:将矩形纸片AOCB折叠,使点C与点A重合,点B落在点B′处(如图),折痕为EF.小明发现△AEF为等腰三角形,你同意吗?请说明理由.
(2)实践与应用:以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,若顶点B的坐标为(9,3),请求出折痕EF的长及EF所在直线的函数关系式.
(1)同意,理由见解析;(2) ,y=3x-12.
,y=3x-12.
解析试题分析:(1)同意.
理由:因为AB∥OC,所以∠AEF=∠EFC.根据折叠性质,有∠AFE=∠EFC.所以∠AEF=∠AFE,AE=AF.△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.设OF=x,则CF=9-x;由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2即:32+x2=(9-x)2,解得x=4,AE=AF=9-x=5,FG=OG-OF=5-4=1.在Rt△EFG中,EF2=EG2+FG2=10,求出EF=
设直线EF的解析式为y=kx+b(k≠0),因为点E(5,3)和点F(4,0)在直线EF上,所以,代入解得解得k,b,进而求出解析式.
试题解析:(1)同意.
理由:∵AB∥OC,∴∠AEF=∠EFC.
根据折叠性质,有∠AFE=∠EFC.
∴∠AEF=∠AFE,
∴AE=AF.
∴△AEF为等腰三角形.
(2)过点E作EG⊥OC于点G.
设OF=x,则CF=9-x;
由折叠可知:AF=9-x.
在Rt△AOF中,AF2=AO2+OF2
∴32+x2=(9-x)2,
∴x=4,9-x=5.
∴AE=AF=5,
∴FG=OG-OF=5-4=1.
在Rt△EFG中,
EF2=EG2+FG2=10,
∴EF=
设直线EF的解析式为y=kx+b(k≠0),
∵点E(5,3)和点F(4,0)在直线EF上,
∴3=5k+b,0=4k+b,
解得:k=3,b=-12.
∴y=3x-12.
考点:1.折叠问题.2.一次函数的解析式.3.勾股定理.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案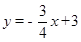 与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.
与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.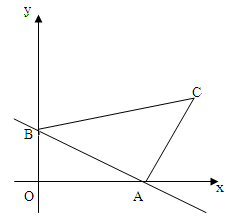
 、
、 (单位:元)与正常运营时间
(单位:元)与正常运营时间 (单位:天)之间分别满足关系式:
(单位:天)之间分别满足关系式: 、
、 ,如图所示.
,如图所示.
 = 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本.
= 元,每辆车的改装费b= 元.正常运营 天后,就可以从节省燃料费中收回改装成本. 与反比例函数
与反比例函数 的图象相交于点A,且点A的纵坐标为1.
的图象相交于点A,且点A的纵坐标为1.
 .当且仅当a=b时,“=”成立.
.当且仅当a=b时,“=”成立. ,∴
,∴ .
. 的最小值.
的最小值. .当且仅当
.当且仅当 ,即x=1时,“=”成立.
,即x=1时,“=”成立. 升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.
升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.